Multiple Approaches to Binary Search

One of the most important parts of programming is being able to find data.

What if the array is really long, and the value we're looking for is at the very end of the array? We are iterating over every single element in the array to find our target at the end... That's so much work! This is where binarySearch comes in.

How Binary Search Works

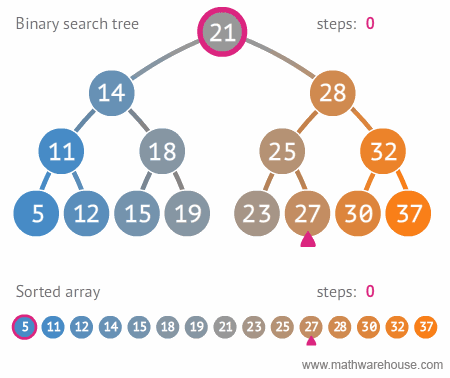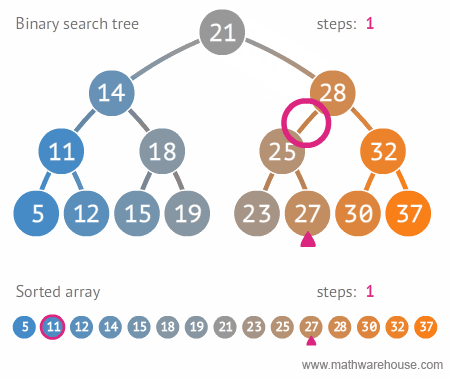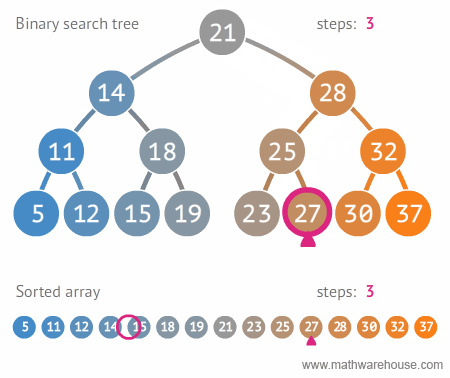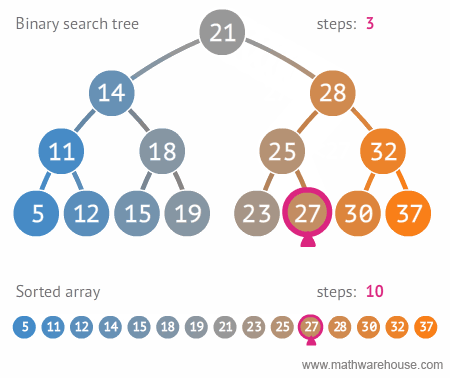
binarySearch employs some simple logic to achieve the same goal in much less time. As the name suggests, binarySearch aims to split a sorted data structure into two halves. Then, it compares the target value to the point where the data was split. It repeats this process, halving the search space each time, until either the item is found or we've run out of data.

If that sounds complicated, think about a real world example: a dictionary. A dictionary contains alphabetically sorted words and their definitions. A dictionary is pretty much only useful if it is ordered in this way. Let's say you wanted to look up the definition of "stupendous." What steps might you take?

• you open up the dictionary at the roughly middle page
• you land in the "m" section
• you know "s" comes somewhere after "m" in the book, so you disregard all pages before the "m" section. Instead, you flip to the roughly middle page between "m" and "z"
• you land in the "u" section
• you know "s" comes somewhere before "u", so you can disregard all pages after the "u" section. Instead, you flip to the roughly middle page between the previous "m" page and "u"
• ...repeat...

You are essentially using the binarySearch algorithm in the real world. Think of the time saved by not flipping through every single page of the dictionary!

Formally, our binarySearch will seek to solve the following problems:

Given a sorted array of numbers and a target num, return a boolean indicating
whether or not that target is contained in the array.

binarySearch([5, 10, 12, 15, 20, 30, 70], 12);  // => true
binarySearch([5, 10, 12, 15, 20, 30, 70], 24);  // => false

Given a sorted array of numbers and a target num, return the index value of the
target if it is contained in the array, and -1 if it is not.

binarySearch([5, 10, 12, 15, 20, 30, 70], 12);  // => 2
binarySearch([5, 10, 12, 15, 20, 30, 70], 24);  // => -1

Important Note on Sorting

binarySearch will only work if the data has been sorted.

Given the dictionary example above, you can see how quickly things would go off the rails if the "s" section containing "stupendous" were placed before the "m" section. If this were the case, our binarySearch method would never be able to find our target word, because we would only ever search the section "m" through "z". Today, know that all arrays in your test cases have already been sorted.

Project Details

Implement binarySearch in five different ways. Like all things in programming, there are multiple ways of doing the same thing, and today's project is about implementing the code, and analyzing the costs/benefits of each implementation.

You will be asked to write five functions: three recursive implementations and two iterative implementations of binarySearch. One of each implementation will return a boolean value indicating whether or not the targetNum was found within the nums array. The remaining three will return the index of the targetNum within the nums array, or a -1 if it is not found. These functions will model the return values of both .includes() and .indexOf(), but employ the more efficient binary search methodology. How cool!

Instructions

• Write your code implementations in the bsearch.js file
• Test your work against the expected results by running node results.js inside the terminal.
• After you've implemented all five functions, discuss with your partner: which is your favorite implementation? Do any seem more or less efficient than the others? Why?