- Write a program to reverse an array or string
- Maximum and minimum of an array using minimum number of comparisons
- Kth smallest element
- Sort an array of 0s, 1s and 2s
- Move all negative numbers to beginning and positive to end with constant extra space
- Union of two arrays
- Cyclically rotate an array by one
- Kadane's Algorithm
- Minimise the maximum difference between heights [V.IMP]
- Minimum no. of Jumps to reach end of an array
- 287. find duplicate in an array of N+1 Integers
- Merge 2 sorted arrays without using Extra space
- 56. Merge Intervals
- 31. Next Permutation
- Count Inversions
- 121. Best Time to Buy and Sell Stock
- find all pairs on integer array whose sum is equal to given number
- find common elements In 3 sorted arrays
- Rearrange array in alternating positive & negative items with O(1) extra space
- Find if there is any subarray with sum equal to 0
- Factorials of large numbers
- Maximum Product Subarray
- Longest consecutive subsequence
- Given an array of size n and a number k, find all elements that appear more than n/k times
- Maximum profit by buying and selling a share at most twice
- Find whether an array is a subset of another array
- Find the triplet that sum to a given value
- Trapping Rain water problem
- Chocolate Distribution Problem
- Smallest Subarray with sum greater than a given value
- Three way partitioning of an array around a given value
- Minimum swaps required bring elements less equal K together
- Palindromic Array
- Find minimum number of merge operations to make an array palindrome
- Median of two sorted arrays of same size
- Median of two sorted arrays of different sizes
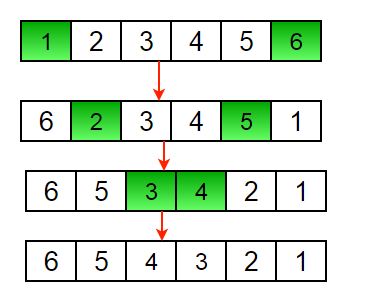
Write a program to reverse an array or string
Given an array (or string), the task is to reverse the array/string.
Examples :
Input : arr[] = {1, 2, 3}
Output : arr[] = {3, 2, 1}
Input : arr[] = {4, 5, 1, 2}
Output : arr[] = {2, 1, 5, 4}
Iterative way :
1) Initialize start and end indexes as start = 0, end = n-1 2) In a loop, swap arr[start] with arr[end] and change start and end as follows : start = start +1, end = end – 1
Another example to reverse a string:
Below is the implementation of the above approach :
// Iterative C++ program to reverse an array
#include <bits/stdc++.h>
using namespace std;
/* Function to reverse arr[] from start to end*/
void rvereseArray(int arr[], int start, int end)
{
while (start < end)
{
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
start++;
end--;
}
}
/* Utility function to print an array */
void printArray(int arr[], int size)
{
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
/* Driver function to test above functions */
int main()
{
int arr[] = {1, 2, 3, 4, 5, 6};
int n = sizeof(arr) / sizeof(arr[0]);
// To print original array
printArray(arr, n);
// Function calling
rvereseArray(arr, 0, n-1);
cout << "Reversed array is" << endl;
// To print the Reversed array
printArray(arr, n);
return 0;
}Output :
1 2 3 4 5 6 Reversed array is 6 5 4 3 2 1
- Time Complexity : O(n)
Recursive Way :
1) Initialize start and end indexes as start = 0, end = n-1 2) Swap arr[start] with arr[end] 3) Recursively call reverse for rest of the array.
Below is the implementation of the above approach :
// Recursive C++ program to reverse an array
#include <bits/stdc++.h>
using namespace std;
/* Function to reverse arr[] from start to end*/
void rvereseArray(int arr[], int start, int end)
{
if (start >= end)
return;
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
// Recursive Function calling
rvereseArray(arr, start + 1, end - 1);
}
/* Utility function to print an array */
void printArray(int arr[], int size)
{
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
/* Driver function to test above functions */
int main()
{
int arr[] = {1, 2, 3, 4, 5, 6};
// To print original array
printArray(arr, 6);
// Function calling
rvereseArray(arr, 0, 5);
cout << "Reversed array is" << endl;
// To print the Reversed array
printArray(arr, 6);
return 0;
}Output :
1 2 3 4 5 6 Reversed array is 6 5 4 3 2 1
Time Complexity : O(n)
Maximum and minimum of an array using minimum number of comparisons
Write a C function to return minimum and maximum in an array. Your program should make the minimum number of comparisons.
// C++ program of above implementation
#include<iostream>
using namespace std;
// Pair struct is used to return
// two values from getMinMax()
struct Pair
{
int min;
int max;
};
Pair getMinMax(int arr[], int n)
{
struct Pair minmax;
int i;
// If there is only one element
// then return it as min and max both
if (n == 1)
{
minmax.max = arr[0];
minmax.min = arr[0];
return minmax;
}
// If there are more than one elements,
// then initialize min and max
if (arr[0] > arr[1])
{
minmax.max = arr[0];
minmax.min = arr[1];
}
else
{
minmax.max = arr[1];
minmax.min = arr[0];
}
for(i = 2; i < n; i++)
{
if (arr[i] > minmax.max)
minmax.max = arr[i];
else if (arr[i] < minmax.min)
minmax.min = arr[i];
}
return minmax;
}
// Driver code
int main()
{
int arr[] = { 1000, 11, 445, 1, 330, 3000 };
int arr_size = 6;
struct Pair minmax = getMinMax(arr, arr_size);
cout << "Minimum element is "
<< minmax.min << endl;
cout << "Maximum element is "
<< minmax.max;
return 0;
}
Output:
Minimum element is 1 Maximum element is 3000
- Time Complexity: O(n)
- Auxiliary Space: O(1) as no extra space was needed.
Divide the array into two parts and compare the maximums and minimums of the two parts to get the maximum and the minimum of the whole array.
Pair MaxMin(array, array_size)
if array_size = 1
return element as both max and min
else if arry_size = 2
one comparison to determine max and min
return that pair
else /* array_size > 2 */
recur for max and min of left half
recur for max and min of right half
one comparison determines true max of the two candidates
one comparison determines true min of the two candidates
return the pair of max and min
Implementation :
// C++ program of above implementation
#include<iostream>
using namespace std;
// structure is used to return
// two values from minMax()
struct Pair
{
int min;
int max;
};
struct Pair getMinMax(int arr[], int low, int high)
{
struct Pair minmax, mml, mmr;
int mid;
// If there is only one element
if (low == high)
{
minmax.max = arr[low];
minmax.min = arr[low];
return minmax;
}
// If there are two elements
if (high == low + 1)
{
if (arr[low] > arr[high])
{
minmax.max = arr[low];
minmax.min = arr[high];
}
else
{
minmax.max = arr[high];
minmax.min = arr[low];
}
return minmax;
}
// If there are more than 2 elements
mid = (low + high) / 2;
mml = getMinMax(arr, low, mid);
mmr = getMinMax(arr, mid + 1, high);
// Compare minimums of two parts
if (mml.min < mmr.min)
minmax.min = mml.min;
else
minmax.min = mmr.min;
// Compare maximums of two parts
if (mml.max > mmr.max)
minmax.max = mml.max;
else
minmax.max = mmr.max;
return minmax;
}
// Driver code
int main()
{
int arr[] = { 1000, 11, 445, 1, 330, 3000 };
int arr_size = 6;
struct Pair minmax = getMinMax(arr, 0, arr_size - 1);
cout << "Minimum element is "
<< minmax.min << endl;
cout << "Maximum element is "
<< minmax.max;
return 0;
}
Output:
Minimum element is 1 Maximum element is 3000
- Time Complexity: O(n)
- Auxiliary Space: O(log n) as the stack space will be filled for the maximum height of the tree formed during recursive calls same as a binary tree.
If n is odd then initialize min and max as first element.
If n is even then initialize min and max as minimum and maximum of the first two elements respectively.
For rest of the elements, pick them in pairs and compare their
maximum and minimum with max and min respectively.
// C++ program of above implementation
#include<iostream>
using namespace std;
// Structure is used to return
// two values from minMax()
struct Pair
{
int min;
int max;
};
struct Pair getMinMax(int arr[], int n)
{
struct Pair minmax;
int i;
// If array has even number of elements
// then initialize the first two elements
// as minimum and maximum
if (n % 2 == 0)
{
if (arr[0] > arr[1])
{
minmax.max = arr[0];
minmax.min = arr[1];
}
else
{
minmax.min = arr[0];
minmax.max = arr[1];
}
// Set the starting index for loop
i = 2;
}
// If array has odd number of elements
// then initialize the first element as
// minimum and maximum
else
{
minmax.min = arr[0];
minmax.max = arr[0];
// Set the starting index for loop
i = 1;
}
// In the while loop, pick elements in
// pair and compare the pair with max
// and min so far
while (i < n - 1)
{
if (arr[i] > arr[i + 1])
{
if(arr[i] > minmax.max)
minmax.max = arr[i];
if(arr[i + 1] < minmax.min)
minmax.min = arr[i + 1];
}
else
{
if (arr[i + 1] > minmax.max)
minmax.max = arr[i + 1];
if (arr[i] < minmax.min)
minmax.min = arr[i];
}
// Increment the index by 2 as
// two elements are processed in loop
i += 2;
}
return minmax;
}
// Driver code
int main()
{
int arr[] = { 1000, 11, 445, 1, 330, 3000 };
int arr_size = 6;
Pair minmax = getMinMax(arr, arr_size);
cout << "nMinimum element is "
<< minmax.min << endl;
cout << "nMaximum element is "
<< minmax.max;
return 0;
}Output:
Minimum element is 1 Maximum element is 3000
Time Complexity: O(n) Auxiliary Space: O(1) as no extra space was needed.
Kth smallest element
Given an array arr[] and an integer K where K is smaller than size of array, the task is to find the Kth smallest element in the given array. It is given that all array elements are distinct.
Example 1:
Input:
N = 6
arr[] = 7 10 4 3 20 15
K = 3
Output : 7
Explanation :
3rd smallest element in the given
array is 7.
Example 2:
Input:
N = 5
arr[] = 7 10 4 20 15
K = 4
Output : 15
Explanation :
4th smallest element in the given array is 15.
Your Task:
You don't have to read input or print anything. Your task is to complete the function kthSmallest() which takes the array arr[], integers l and r denoting the starting and ending index of the array and an integer K as input and returns the Kth smallest element.
Expected Time Complexity: O(n) Expected Auxiliary Space: O(log(n))
- Constraints:
1 <= N <= 10^5
1 <= arr[i] <= 10^5
1 <= K <= N
#include<bits/stdc++.h>
using namespace std;
// } Driver Code Ends
//User function template for C++
class Solution{
public:
void swap(int *a, int *b){
int temp = *a;
*a = *b;
*b = temp;
}
int randomPartition(int arr[], int l, int r){
int n = r-l+1;
int pivot = rand()%n;
swap(&arr[l+pivot],&arr[r]);
return partition(arr,l,r);
}
int kthSmallest(int arr[], int l, int r, int k) {
if(k>0 && k<=r-l+1){
int pos = randomPartition(arr,l,r);
if(pos-l == k-1){
return arr[pos];
}
if(pos-l>k-1){
return kthSmallest(arr,l,pos-1,k);
}
return kthSmallest(arr,pos+1,r,k-pos+l-1);
}
return INT_MAX;
}
int partition(int arr[],int l, int r){
int x = arr[r],i=l;
for (int j=l;j<=r-1;j++){
if(arr[j]<=x){
swap(&arr[i], &arr[j]);
i++;
}
}
swap(&arr[i],&arr[r]);
return i;
}
};
// { Driver Code Starts.
int main()
{
int test_case;
cin>>test_case;
while(test_case--)
{
int number_of_elements;
cin>>number_of_elements;
int a[number_of_elements];
for(int i=0;i<number_of_elements;i++)
cin>>a[i];
int k;
cin>>k;
Solution ob;
cout<<ob.kthSmallest(a, 0, number_of_elements-1, k)<<endl;
}
return 0;
}Sort an array of 0s, 1s and 2s
Given an array of size N containing only 0s, 1s, and 2s; sort the array in ascending order.
Example 1:
Input:
N = 5
arr[]= {0 2 1 2 0}
Output:
0 0 1 2 2
Explanation:
0s 1s and 2s are segregated into ascending order.
Example 2:
Input:
N = 3
arr[] = {0 1 0}
Output:
0 0 1
Explanation:
0s 1s and 2s are segregated into ascending order.
Your Task:
You don't need to read input or print anything. Your task is to complete the function sort012() that takes an array arr and N as input parameters and sorts the array in-place.
Expected Time Complexity: O(N) Expected Auxiliary Space: O(1)
- Constraints:
1 <= N <= 10^6
0 <= A[i] <= 2
#include<bits/stdc++.h>
using namespace std;
// } Driver Code Ends
class Solution
{
public:
void sort012(int a[], int n)
{
// coode here
int low = 0, high = n-1, mid = 0;
while(mid <= high){
if(a[mid]==0)
swap(a[mid++], a[low++]);
else if(a[mid]==1)
mid++;
else
swap(a[mid], a[high--]);
}
}
};
// { Driver Code Starts.
int main() {
int t;
cin >> t;
while(t--){
int n;
cin >>n;
int a[n];
for(int i=0;i<n;i++){
cin >> a[i];
}
Solution ob;
ob.sort012(a, n);
for(int i=0;i<n;i++){
cout << a[i] << " ";
}
cout << endl;
}
return 0;
}Move all negative numbers to beginning and positive to end with constant extra space
An array contains both positive and negative numbers in random order. Rearrange the array elements so that all negative numbers appear before all positive numbers.
Examples :
Input: -12, 11, -13, -5, 6, -7, 5, -3, -6 Output: -12 -13 -5 -7 -3 -6 11 6 5
Note: Order of elements is not important here.
The idea is to simply apply the partition process of quicksort.
// A C++ program to put all negative
// numbers before positive numbers
#include <bits/stdc++.h>
using namespace std;
void rearrange(int arr[], int n)
{
int j = 0;
for (int i = 0; i < n; i++) {
if (arr[i] < 0) {
if (i != j)
swap(arr[i], arr[j]);
j++;
}
}
}
// A utility function to print an array
void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
}
// Driver code
int main()
{
int arr[] = { -1, 2, -3, 4, 5, 6, -7, 8, 9 };
int n = sizeof(arr) / sizeof(arr[0]);
rearrange(arr, n);
printArray(arr, n);
return 0;
}Output:
-1 -3 -7 4 5 6 2 8 9
- Time complexity: O(N)
- Auxiliary Space: O(1)
The idea is to solve this problem with constant space and linear time is by using a two-pointer or two-variable approach where we simply take two variables like left and right which hold the 0 and N-1 indexes. Just need to check that :
Check If the left and right pointer elements are negative then simply increment the left pointer.
Otherwise, if the left element is positive and the right element is negative then simply swap the elements, and simultaneously increment and decrement the left and right pointers.
Else if the left element is positive and the right element is also positive then simply decrement the right pointer.
Repeat the above 3 steps until the left pointer ≤ right pointer.
Below is the implementation of the above approach:
// C++ program of the above
// approach
#include <iostream>
using namespace std;
// Function to shift all the
// negative elements on left side
void shiftall(int arr[], int left,
int right)
{
// Loop to iterate over the
// array from left to the right
while (left<=right)
{
// Condition to check if the left
// and the right elements are
// negative
if (arr[left] < 0 && arr[right] < 0)
left+=1;
// Condition to check if the left
// pointer element is positive and
// the right pointer element is negative
else if (arr[left]>0 && arr[right]<0)
{
int temp=arr[left];
arr[left]=arr[right];
arr[right]=temp;
left+=1;
right-=1;
}
// Condition to check if both the
// elements are positive
else if (arr[left]>0 && arr[right] >0)
right-=1;
else{
left += 1;
right -= 1;
}
}
}
// Function to print the array
void display(int arr[], int right){
// Loop to iterate over the element
// of the given array
for (int i=0;i<=right;++i){
cout<<arr[i]<<" ";
}
cout<<endl;
}
// Driver Code
int main()
{
int arr[] = {-12, 11, -13, -5,
6, -7, 5, -3, 11};
int arr_size = sizeof(arr) /
sizeof(arr[0]);
// Function Call
shiftall(arr,0,arr_size-1);
display(arr,arr_size-1);
return 0;
}
Output :
-12 -3 -13 -5 -7 6 5 11 11
This is an in-place rearranging algorithm for arranging the positive and negative numbers where the order of elements is not maintained.
- Time Complexity: O(N)
- Auxiliary Space: O(1)
Here, we will use the famous Dutch National Flag Algorithm for two “colors”. The first color will be for all negative integers and the second color will be for all positive integers. We will divide the array into three partitions with the help of two pointers, low and high.
- ar[1…low-1] negative integers
- ar[low…high] unknown
- ar[high+1…N] positive integers
Now, we explore the array with the help of low pointer, shrinking the unknown partition, and moving elements to their correct partition in the process. We do this until we have explored all the elements, and size of the unknown partition shrinks to zero.
Below is the implementation of the above approach:
#include <iostream>
using namespace std;
// Swap Function.
void swap(int &a,int &b){
int temp =a;
a=b;
b=temp;
}
// Using Dutch National Flag Algorithm.
void reArrange(int arr[],int n){
int low =0,high = n-1;
while(low<high){
if(arr[low]<0){
low++;
}else if(arr[high]>0){
high--;
}else{
swap(arr[low],arr[high]);
}
}
}
void displayArray(int arr[],int n){
for(int i=0;i<n;i++){
cout<<arr[i]<<" ";
}
cout<<endl;
}
int main() {
// Data
int arr[] = {1, 2, -4, -5, 2, -7, 3, 2, -6, -8, -9, 3, 2, 1};
int n = sizeof(arr)/sizeof(arr[0]);
reArrange(arr,n);
displayArray(arr,n);
return 0;
}Output:
-9 -8 -4 -5 -6 -7 3 2 2 2 1 3 2 1
- Time complexity: O(N)
- Auxiliary Space: O(1)
The order of elements does not matter here.
Union of two arrays
Given two arrays a[] and b[] of size n and m respectively. The task is to find union between these two arrays.
Union of the two arrays can be defined as the set containing distinct elements from both the arrays. If there are repetitions, then only one occurrence of element should be printed in the union.
Example 1:
Input:
5 3
1 2 3 4 5
1 2 3
Output:
5
Explanation:
1, 2, 3, 4 and 5 are the elements which comes in the union set of both arrays. So count is 5.
Example 2:
Input:
6 2
85 25 1 32 54 6
85 2
Output:
7
Explanation:
85, 25, 1, 32, 54, 6, and 2 are the elements which comes in the union set of both arrays. So count is 7.
Your Task:
Complete doUnion funciton that takes a, n, b, m as parameters and returns the count of union elements of the two arrays. The printing is done by the driver code.
- Constraints:
1 ≤ n, m ≤ 10^5
0 ≤ a[i], b[i] < 10^5
Expected Time Complexity : O((n+m)log(n+m)) Expected Auxilliary Space : O(n+m)
#include <bits/stdc++.h>
using namespace std;
// } Driver Code Ends
//User function template in C++
class Solution{
public:
//Function to return the count of number of elements in union of two arrays.
int doUnion(int a[], int n, int b[], int m) {
//code here
//using set to store the elements.
unordered_set<int> s;
//we insert all the elements of first array in set.
for(int i = 0;i<n;i++)
s.insert(a[i]);
//we insert all the elements of second array in set.
//Set does not contain duplicates.
for(int i = 0;i<m;i++)
s.insert(b[i]);
//returning the size of set which is total number of elements in set.
return s.size() ;
}
};
// { Driver Code Starts.
int main() {
int t;
cin >> t;
while(t--){
int n, m;
cin >> n >> m;
int a[n], b[m];
for(int i = 0;i<n;i++)
cin >> a[i];
for(int i = 0;i<m;i++)
cin >> b[i];
Solution ob;
cout << ob.doUnion(a, n, b, m) << endl;
}
return 0;
} Cyclically rotate an array by one
Given an array, rotate the array by one position in clock-wise direction.
Example 1:
Input:
N = 5
A[] = {1, 2, 3, 4, 5}
Output:
5 1 2 3 4
Example 2:
Input:
N = 8
A[] = {9, 8, 7, 6, 4, 2, 1, 3}
Output:
3 9 8 7 6 4 2 1
Your Task:
You don't need to read input or print anything. Your task is to complete the function rotate() which takes the array A[] and its size N as inputs and modify the array.
Expected Time Complexity: O(N) Expected Auxiliary Space: O(1)
- Constraints:
1<=N<=10^5
0<=a[i]<=10^5
#include <bits/stdc++.h>
using namespace std;
void rotate(int arr[], int n);
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
int a[n] , i;
for(i=0;i<n;i++)
scanf("%d",&a[i]);
rotate(a, n);
for (i = 0; i < n; i++)
printf("%d ", a[i]);
printf("\n");
}
return 0;
}
// } Driver Code Ends
//User function Template for C++
void rotate(int arr[], int n)
{
int x = arr[n-1], i;
for (i = n-1; i > 0; i--)arr[i] = arr[i-1];
arr[0] = x;
}Kadane's Algorithm
Given an array Arr[] of N integers. Find the contiguous sub-array(containing at least one number) which has the maximum sum and return its sum.
Example 1:
Input:
N = 5
Arr[] = {1,2,3,-2,5}
Output:
9
Explanation:
Max subarray sum is 9 of elements (1, 2, 3, -2, 5) which is a contiguous subarray.
Example 2:
Input:
N = 4
Arr[] = {-1,-2,-3,-4}
Output:
-1
Explanation:
Max subarray sum is -1 of element (-1)
Your Task:
You don't need to read input or print anything. The task is to complete the function maxSubarraySum() which takes Arr[] and N as input parameters and returns the sum of subarray with maximum sum.
Expected Time Complexity: O(N) Expected Auxiliary Space: O(1)
- Constraints:
1 ≤ N ≤ 10^6
-10^7 ≤ A[i] ≤ 10^7
#include<bits/stdc++.h>
using namespace std;
// } Driver Code Ends
class Solution{
public:
long long maxSubarraySum(int arr[], int n){
long long maxh = 0, maxf = arr[0];
for(int i=0;i<n;i++){
maxh+=arr[i];
if(maxf<maxh)maxf=maxh;
if(maxh<0)maxh=0;
}
return maxf;
}
};
// { Driver Code Starts.
int main()
{
int t,n;
cin>>t; //input testcases
while(t--) //while testcases exist
{
cin>>n; //input size of array
int a[n];
for(int i=0;i<n;i++)
cin>>a[i]; //inputting elements of array
Solution ob;
cout << ob.maxSubarraySum(a, n) << endl;
}
}Minimise the maximum difference between heights [V.IMP]
Given an array arr[] denoting heights of N towers and a positive integer K, you have to modify the height of each tower either by increasing or decreasing them by K only once. After modifying, height should be a non-negative integer.
Find out the minimum possible difference of the height of shortest and longest towers after you have modified each tower.
Note: It is compulsory to increase or decrease by K to each tower.
Example 1:
Input:
K = 2, N = 4
Arr[] = {1, 5, 8, 10}
Output:
5
Explanation:
The array can be modified as {3, 3, 6, 8}. The difference between the largest and the smallest is 8-3 = 5.
Example 2:
Input:
K = 3, N = 5
Arr[] = {3, 9, 12, 16, 20}
Output:
11
Explanation:
The array can be modified as {6, 12, 9, 13, 17}. The difference between the largest and the smallest is 17-6 = 11.
Your Task:
You don't need to read input or print anything. Your task is to complete the function getMinDiff() which takes the arr[], n and k as input parameters and returns an integer denoting the minimum difference.
Expected Time Complexity: O(N*logN) Expected Auxiliary Space: O(N)
- Constraints :
1 ≤ K ≤ 10^4
1 ≤ N ≤ 10^5
1 ≤ Arr[i] ≤ 10^5
#include <bits/stdc++.h>
using namespace std;
// } Driver Code Ends
// User function template for C++
class Solution {
public:
int getMinDiff(int arr[], int n, int k) {
// code here
vector<pair<int, int>> v;
vector<int> taken(n);
// we will store all possible heights in a vector
for (int i = 0; i < n; i++) {
if (arr[i] - k >= 0) {
v.push_back({arr[i] - k, i});
}
v.push_back({arr[i] + k, i});
}
sort(v.begin(), v.end());
int elements_in_range = 0;
int left = 0;
int right = 0;
// By two pointer we will traverse v and whenever we will get a range
// in which all towers are included, we will update the answer.
while (elements_in_range < n && right < v.size()) {
if (taken[v[right].second] == 0) {
elements_in_range++;
}
taken[v[right].second]++;
right++;
}
int ans = v[right - 1].first - v[left].first;
while (right < v.size()) {
if (taken[v[left].second] == 1) {
elements_in_range--;
}
taken[v[left].second]--;
left++;
while (elements_in_range < n && right < v.size()) {
if (taken[v[right].second] == 0) {
elements_in_range++;
}
taken[v[right].second]++;
right++;
}
if (elements_in_range == n) {
ans = min(ans, v[right - 1].first - v[left].first);
} else {
break;
}
}
return ans;
}
};
// { Driver Code Starts.
int main() {
int t;
cin >> t;
while (t--) {
int n, k;
cin >> k;
cin >> n;
int arr[n];
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
Solution ob;
auto ans = ob.getMinDiff(arr, n, k);
cout << ans << "\n";
}
return 0;
} Minimum no. of Jumps to reach end of an array
Given an array of N integers arr[] where each element represents the max number of steps that can be made forward from that element. Find the minimum number of jumps to reach the end of the array (starting from the first element). If an element is 0, then you cannot move through that element.
Note: Return -1 if you can't reach the end of the array.
Example 1:
Input:
N = 11
arr[] = {1, 3, 5, 8, 9, 2, 6, 7, 6, 8, 9}
Output: 3
Explanation:
First jump from 1st element to 2nd element with value 3. Now, from here we jump to 5th element with value 9, and from here we will jump to last.
Example 2:
Input :
N = 6
arr = {1, 4, 3, 2, 6, 7}
Output: 2
Explanation: First we jump from the 1st to 2nd element and then jump to the last element.
Your task:
You don't need to read input or print anything. Your task is to complete function minJumps() which takes the array arr and it's size N as input parameters and returns the minimum number of jumps. If not possible returns -1.
Expected Time Complexity: O(N) Expected Space Complexity: O(1)
- Constraints:
1 ≤ N ≤ 10^7
0 ≤ arri ≤ 10^7
#include<bits/stdc++.h>
using namespace std;
// } Driver Code Ends
// Function to return minimum number of jumps to end of array
class Solution{
public:
int minJumps(int arr[], int n){
if(n<=1)return 0;
if(arr[0]==0)return -1;
int maxreach = arr[0];
int step = arr[0];
int jump = 1;
for(int i=1;i<n;i++){
if(i==n-1)return jump;
maxreach = max(maxreach,i+arr[i]);
step--;
if(step==0){
jump++;
if(i>=maxreach)return -1;
step = maxreach -i ;
}
}
return -1;
}
};
// { Driver Code Starts.
int main()
{
int t;
cin>>t;
while(t--)
{
int n,i,j;
cin>>n;
int arr[n];
for(int i=0; i<n; i++)
cin>>arr[i];
Solution obj;
cout<<obj.minJumps(arr, n)<<endl;
}
return 0;
}287. find duplicate in an array of N+1 Integers
Given an array of integers nums containing n + 1 integers where each integer is in the range [1, n] inclusive.
There is only one repeated number in nums, return this repeated number.
You must solve the problem without modifying the array nums and uses only constant extra space.
Example 1:
Input: nums = [1,3,4,2,2]
Output: 2
Example 2:
Input: nums = [3,1,3,4,2]
Output: 3
- Constraints:
1 <= n <= 10^5
nums.length == n + 1
1 <= nums[i] <= n
All the integers innumsappear only once except for precisely one integer which appears two or more times.
class Solution {
public:
// Tortoise and hare Method TC - O(N) SC - O(1)
int findDuplicate(vector<int>& arr)
{
int slow, fast;
slow = arr[0], fast = arr[0];
do {
slow = arr[slow];
fast = arr[arr[fast]];
}while(slow != fast);
fast = arr[0];
while(slow != fast) {
slow = arr[slow];
fast = arr[fast];
}
return slow;
}
/*
// Hashing Technique TC - O(N) SC - O(N)
int findDuplicate(vector<int>& arr)
{
map<int,int>mp;
for(int i = 0; i < arr.size(); i++) {
if(mp.find(arr[i]) == mp.end()) {
mp[arr[i]]++;
}
else
return arr[i];
}
return -1;
}
*/Merge 2 sorted arrays without using Extra space.
Given two sorted arrays arr1[] of size N and arr2[] of size M. Each array is sorted in non-decreasing order. Merge the two arrays into one sorted array in non-decreasing order without using any extra space.
Example 1:
Input:
N = 4, M = 5
arr1[] = {1, 3, 5, 7}
arr2[] = {0, 2, 6, 8, 9}
Output: 0 1 2 3 5 6 7 8 9
Explanation: Since you can't use any extra space, modify the given arrays to form
arr1[] = {0, 1, 2, 3}
arr2[] = {5, 6, 7, 8, 9}
Example 2:
Input:
N = 2, M = 3
arr1[] = {10, 12}
arr2[] = {5, 18, 20}
Output: 5 10 12 18 20
Explanation: Since you can't use any extra space, modify the given arrays to form
arr1[] = {5, 10}
arr2[] = {12, 18, 20}
Your Task:
You don't need to read input or print anything. Complete the function merge() which takes the two arrays arr1[], arr2[] and their sizes n and m, as input parameters. The function does not return anything. Use the given arrays to sort and merge arr1[] and arr2[] in-place.
Note: The generated output will print all the elements of arr1[] followed by all the elements of arr2[].
Expected Time Complexity: O((n+m)*log(n+m)) Expected Auxiliary Space: O(1)
- Constraints:
1 <= N, M <= 5*10^4
0 <= arr1i, arr2i <= 10^6
class Solution{
public:
int nextGap(int gap){
if(gap<=1)
return 0;
return (gap/2)+(gap%2);
}
void merge(int arr1[], int arr2[], int n, int m) {
// code here
//already done in array part
int i, j, gap = n+m;
for(gap = nextGap(gap); gap>0; gap=nextGap(gap)){
// comparing elements in the first array itself with difference in
// index equal to the value of the gap.
for(i = 0; i + gap < n; i++)
// if element at ith index is greater than element at
// (i+gap)th index, we swap them.
if(arr1[i]>arr1[i+gap])
swap(arr1[i],arr1[i+gap]);
// now comparing elements in both arrays with help of two pointers.
// the loop stops whenever any pointer exceeds the size of its array.
for(j = gap > n? gap-n : 0 ; i < n&&j < m; i++, j++)
// if element in the first array is greater than element in
// second array, we swap them.
if(arr1[i] > arr2[j])
swap(arr1[i], arr2[j]);
if(j<m){
// at last, comparing elements in the second array itself with
// difference in index equal to the value of the gap.
for(j = 0 ; j+gap < m ; j++)
// if element at jth index is greater than element at
// (j+gap)th index, we swap them.
if(arr2[j]>arr2[j+gap])
swap(arr2[j],arr2[j+gap]);
}
}
}
};
// { Driver Code Starts.
int main() {
int t;
cin >> t;
while (t--) {
int n, m, i;
cin >> n >> m;
int arr1[n], arr2[m];
for (i = 0; i < n; i++) {
cin >> arr1[i];
}
for (i = 0; i < m; i++) {
cin >> arr2[i];
}
Solution ob;
ob.merge(arr1, arr2, n, m);
for (i = 0; i < n; i++) {
cout << arr1[i] << " ";
}
for (i = 0; i < m; i++) {
cout << arr2[i] << " ";
}
cout << "\n";
}
return 0;
}56. Merge Intervals
Given an array of intervals where intervals[i] = [starti, endi], merge all overlapping intervals, and return an array of the non-overlapping intervals that cover all the intervals in the input.
Example 1:
Input: intervals = [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3] and [2,6] overlaps, merge them into [1,6].
Example 2:
Input: intervals = [[1,4],[4,5]]
Output: [[1,5]]
Explanation: Intervals [1,4] and [4,5] are considered overlapping.
- Constraints:
1 <= intervals.length <= 10^4
intervals[i].length == 2
0 <= starti <= endi <= 10^4
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
sort(intervals.begin(), intervals.end());
vector<vector<int>> merged;
for (auto interval : intervals) {
// if the list of merged intervals is empty or if the current
// interval does not overlap with the previous, simply append it.
if (merged.empty() || merged.back()[1] < interval[0]) {
merged.push_back(interval);
}
// otherwise, there is overlap, so we merge the current and previous
// intervals.
else {
merged.back()[1] = max(merged.back()[1], interval[1]);
}
}
return merged;
}
};31. Next Permutation
A permutation of an array of integers is an arrangement of its members into a sequence or linear order.
- For example, for
arr = [1,2,3], the following are considered permutations ofarr: [1,2,3],[1,3,2],[3,1,2],[2,3,1].
The next permutation of an array of integers is the next lexicographically greater permutation of its integer. More formally, if all the permutations of the array are sorted in one container according to their lexicographical order, then the next permutation of that array is the permutation that follows it in the sorted container. If such arrangement is not possible, the array must be rearranged as the lowest possible order (i.e., sorted in ascending order).
- For example, the next permutation of
arr = [1,2,3]is[1,3,2]. - Similarly, the next permutation of
arr = [2,3,1]is[3,1,2]. - While the next permutation of
arr = [3,2,1]is[1,2,3]because[3,2,1]does not have a lexicographical larger rearrangement.
Given an array of integers nums, find the next permutation of nums.
The replacement must be in place and use only constant extra memory.
Example 1:
Input: nums = [1,2,3]
Output: [1,3,2]
Example 2:
Input: nums = [3,2,1]
Output: [1,2,3]
Example 3:
Input: nums = [1,1,5]
Output: [1,5,1]
- Constraints:
1 <= nums.length <= 100
0 <= nums[i] <= 100
class Solution {
public:
void reverse(vector<int>& nums, int low, int high) {
while(low < high) {
swap(nums[low], nums[high]);
low++;
high--;
}
}
void nextPermutation(vector<int>& nums) {
int n = nums.size();
for (int i = n-1 ; i>=0; i--) {
while(i>0 && nums[i] <= nums[i-1])
i--;
if(i==0) {
sort(nums.begin(), nums.end());
return;
}
int j;
for(j = n-1; j>i ; j--)
if(nums[i-1] < nums[j])
break;
swap(nums[i-1], nums[j]);
reverse(nums, i, n-1);
return;
}
}
};Count Inversions
Given an array of integers. Find the Inversion Count in the array.
Inversion Count: For an array, inversion count indicates how far (or close) the array is from being sorted. If array is already sorted then the inversion count is 0. If an array is sorted in the reverse order then the inversion count is the maximum.
Formally, two elements a[i] and a[j] form an inversion if a[i] > a[j] and i < j.
Example 1:
Input: N = 5, arr[] = {2, 4, 1, 3, 5}
Output: 3
Explanation: The sequence 2, 4, 1, 3, 5 has three inversions (2, 1), (4, 1), (4, 3).
Example 2:
Input: N = 5
arr[] = {2, 3, 4, 5, 6}
Output: 0
Explanation: As the sequence is already sorted so there is no inversion count.
Example 3:
Input: N = 3, arr[] = {10, 10, 10}
Output: 0
Explanation: As all the elements of array are same, so there is no inversion count.
Your Task:
You don't need to read input or print anything. Your task is to complete the function inversionCount() which takes the array arr[] and the size of the array as inputs and returns the inversion count of the given array.
Expected Time Complexity: O(NLogN). Expected Auxiliary Space: O(N).
- Constraints:
1 ≤ N ≤ 5*10^5
1 ≤ arr[i] ≤ 10^18
#include <bits/stdc++.h>
using namespace std;
// } Driver Code Ends
class Solution{
public:
long long my_counter = 0;
// arr[]: Input Array
// N : Size of the Array arr[]
// Function to count inversions in the array.
void mergeSort(long long a[], long long p, long long r){
if(p<r){
long long q = (p+r)/2;
mergeSort(a, p, q);
mergeSort(a, q+1, r);
merge(a, p, q, r);
}
}
void merge(long long a[], long long p, long long q, long long r){
long long l = q-p+1;
long long a1[l];
long long l2 = r-q;
long long a2[l2];
for(long long i = 0;i<l;i++){
a1[i] = a[i+p];
}
for(long long i = 0;i<l2;i++){
a2[i] = a[q+i+1];
}
long long left = 0, right = 0, k = p;
while(left<l && right < l2){
if(a1[left] <= a2[right]){
a[k] = a1[left];
left++;
}
else{
a[k] = a2[right];
right++;
my_counter += (l-left);
}
k++;
}
while(left<l){
a[k++] = a1[left++];
}
while(right < l2){
a[k++] = a2[right++];
}
}
long long int inversionCount(long long arr[], long long N)
{
// Your Code Here
mergeSort(arr,0,N-1);
long long int res = my_counter;
my_counter = 0;
return res;
}
};
// { Driver Code Starts.
int main() {
long long T;
cin >> T;
while(T--){
long long N;
cin >> N;
long long A[N];
for(long long i = 0;i<N;i++){
cin >> A[i];
}
Solution obj;
cout << obj.inversionCount(A,N) << endl;
}
return 0;
}121. Best Time to Buy and Sell Stock
You are given an array prices where prices[i] is the price of a given stock on the ith day.
You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.
Example 1:
Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
Example 2:
Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.
- Constraints:
1 <= prices.length <= 10^5
0 <= prices[i] <= 10^4
class Solution {
public:
int maxProfit(vector<int>& prices) {
int profit = 0, minPrice = INT_MAX;
for(int i = 0;i<prices.size();i++){
if(prices[i]<minPrice)minPrice = prices[i];
else if(prices[i]-minPrice > profit)profit = prices[i]-minPrice;
}
return profit;
}
};find all pairs on integer array whose sum is equal to given number
Given an array of N integers, and an integer K, find the number of pairs of elements in the array whose sum is equal to K.
Example 1:
Input:
N = 4, K = 6
arr[] = {1, 5, 7, 1}
Output: 2
Explanation:
arr[0] + arr[1] = 1 + 5 = 6
and arr[1] + arr[3] = 5 + 1 = 6.
Example 2:
Input:
N = 4, K = 2
arr[] = {1, 1, 1, 1}
Output: 6
Explanation:
Each 1 will produce sum 2 with any 1.
Your Task:
You don't need to read input or print anything. Your task is to complete the function getPairsCount() which takes arr[], n and k as input parameters and returns the number of pairs that have sum K.
Expected Time Complexity: O(N) Expected Auxiliary Space: O(N)
- Constraints:
1 <= N <= 10^5
1 <= K <= 10^8
1 <= Arr[i] <= 10^6
#include <bits/stdc++.h>
using namespace std;
//User function template for C++
class Solution{
public:
int getPairsCount(int arr[], int n, int k) {
// code here
unordered_map<int, int>m;
for(int i = 0;i<n;i++)m[arr[i]]++;
int doublecount = 0;
for(int i = 0;i<n;i++){
doublecount += m[k-arr[i]];
if(k-arr[i] == arr[i]) doublecount--;
}
return doublecount/2;
}
};
int main() {
int t;
cin >> t;
while (t--) {
int n, k;
cin >> n >> k;
int arr[n];
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
Solution ob;
auto ans = ob.getPairsCount(arr, n, k);
cout << ans << "\n";
}
return 0;
}find common elements In 3 sorted arrays
Given three arrays sorted in increasing order. Find the elements that are common in all three arrays.
Example 1:
Input:
n1 = 6; A = {1, 5, 10, 20, 40, 80}
n2 = 5; B = {6, 7, 20, 80, 100}
n3 = 8; C = {3, 4, 15, 20, 30, 70, 80, 120}
Output: 20 80
Explanation: 20 and 80 are the only common elements in A, B and C.
Your Task:
You don't need to read input or print anything. Your task is to complete the function commonElements() which take the 3 arrays A[], B[], C[] and their respective sizes n1, n2 and n3 as inputs and returns an array containing the common element present in all the 3 arrays in sorted order.
If there are no such elements return an empty array. In this case the output will be printed as -1.
Expected Time Complexity: O(n1 + n2 + n3) Expected Auxiliary Space: O(n1 + n2 + n3)
- Constraints:
1 <= n1, n2, n3 <= 10^5
The array elements can be bothpositiveornegativeintegers.
#include <bits/stdc++.h>
using namespace std;
class Solution
{
public:
vector <int> commonElements (int A[], int B[], int C[], int n1, int n2, int n3){
int i =0, j=0, k=0;
vector<int>sol;
int check = INT_MIN;
while(i<n1 && j<n2 && k<n3){
if(A[i]==B[j] && A[i]==C[k] && A[i]!=check){
sol.push_back(A[i]);
check = A[i];
i++;j++;k++;
}
else if(min({A[i],B[j],C[k]}) == A[i])i++;
else if(min({A[i],B[j],C[k]}) == B[j])j++;
else k++;
}
return sol;
}
};
int main ()
{
int t; cin >> t;
while (t--)
{
int n1, n2, n3;
cin >> n1 >> n2 >> n3;
int A[n1];
int B[n2];
int C[n3];
for (int i = 0; i < n1; i++) cin >> A[i];
for (int i = 0; i < n2; i++) cin >> B[i];
for (int i = 0; i < n3; i++) cin >> C[i];
Solution ob;
vector <int> res = ob.commonElements (A, B, C, n1, n2, n3);
if (res.size () == 0)
cout << -1;
for (int i = 0; i < res.size (); i++)
cout << res[i] << " ";
cout << endl;
}
}Rearrange array in alternating positive & negative items with O(1) extra space
Given an array of positive and negative numbers, arrange them in an alternate fashion such that every positive number is followed by negative and vice-versa maintaining the order of appearance.
Number of positive and negative numbers need not be equal. If there are more positive numbers they appear at the end of the array. If there are more negative numbers, they too appear in the end of the array.
Examples :
Input: arr[] = {1, 2, 3, -4, -1, 4}
Output: arr[] = {-4, 1, -1, 2, 3, 4}
Input: arr[] = {-5, -2, 5, 2, 4, 7, 1, 8, 0, -8}
output: arr[] = {-5, 5, -2, 2, -8, 4, 7, 1, 8, 0}
The above problem can be easily solved if O(n) extra space is allowed. It becomes interesting due to the limitations that O(1) extra space and order of appearances.
The idea is to process array from left to right. While processing, find the first out of place element in the remaining unprocessed array. An element is out of place if it is negative and at odd index (0 based index), or it is positive and at even index (0 based index) . Once we find an out of place element, we find the first element after it with opposite sign. We right rotate the subarray between these two elements (including these two).
/* C++ program to rearrange
positive and negative integers
in alternate fashion while keeping
the order of positive and negative numbers. */
#include <assert.h>
#include <iostream>
using namespace std;
// Utility function to right rotate all elements between
// [outofplace, cur]
void rightrotate(int arr[], int n, int outofplace, int cur)
{
char tmp = arr[cur];
for (int i = cur; i > outofplace; i--)
arr[i] = arr[i - 1];
arr[outofplace] = tmp;
}
void rearrange(int arr[], int n)
{
int outofplace = -1;
for (int index = 0; index < n; index++)
{
if (outofplace >= 0)
{
// find the item which must be moved into the
// out-of-place entry if out-of-place entry is
// positive and current entry is negative OR if
// out-of-place entry is negative and current
// entry is negative then right rotate
//
// [...-3, -4, -5, 6...] --> [...6, -3, -4,
// -5...]
// ^ ^
// | |
// outofplace --> outofplace
//
if (((arr[index] >= 0) && (arr[outofplace] < 0))
|| ((arr[index] < 0)
&& (arr[outofplace] >= 0)))
{
rightrotate(arr, n, outofplace, index);
// the new out-of-place entry is now 2 steps
// ahead
if (index - outofplace >= 2)
outofplace = outofplace + 2;
else
outofplace = -1;
}
}
// if no entry has been flagged out-of-place
if (outofplace == -1) {
// check if current entry is out-of-place
if (((arr[index] >= 0) && (!(index & 0x01)))
|| ((arr[index] < 0) && (index & 0x01))) {
outofplace = index;
}
}
}
}
// A utility function to print an array 'arr[]' of size 'n'
void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
}
// Driver code
int main()
{
int arr[] = { -5, -2, 5, 2,
4, 7, 1, 8, 0, -8 };
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Given array is \n";
printArray(arr, n);
rearrange(arr, n);
cout << "Rearranged array is \n";
printArray(arr, n);
return 0;
}Output :
Given array is -5 -2 5 2 4 7 1 8 0 -8 Rearranged array is -5 5 -2 2 -8 4 7 1 8 0
Time Complexity : O(N^2), as we are using a loop to traverse N times and calling function rightrotate each time which will cost O (N). Space Complexity : O(1), as we are not using any extra space.
Find if there is any subarray with sum equal to 0
Given an array of positive and negative numbers. Find if there is a subarray (of size at-least one) with 0 sum.
Example 1:
Input:
5
4 2 -3 1 6
Output:
Yes
Explanation:
2, -3, 1 is the subarray with sum 0.
Example 2:
Input:
5
4 2 0 1 6
Output:
Yes
Explanation:
0 is one of the element n the array so there exist a subarray with sum 0.
Your Task:
You only need to complete the function subArrayExists() that takes array and n as parameters and returns true or false depending upon whether there is a subarray present with 0-sum or not. Printing will be taken care by the drivers code.
Expected Time Complexity: O(n). Expected Auxiliary Space: O(n).
- Constraints:
1 <= n <= 10^4
-10^5 <= a[i] <= 10^5
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
bool subArrayExists(int arr[], int n){
unordered_map<int,bool>map;
int sum = 0;
for(int i=0;i<n;i++){
sum+=arr[i];
if(sum == 0 || map[sum] == true)return true;
map[sum] = true;
}
return false;
}
};
int main()
{
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
int arr[n];
for(int i=0;i<n;i++)
cin>>arr[i];
Solution obj;
if (obj.subArrayExists(arr, n))
cout << "Yes\n";
else
cout << "No\n";
}
return 0;
}Factorials of large numbers
Given an integer N, find its factorial.
Example 1:
Input: N = 5
Output: 120
Explanation : 5! = 12345 = 120
Example 2:
Input: N = 10
Output: 3628800
Explanation :
10! = 123456789*10 = 3628800
Your Task:
You don't need to read input or print anything. Complete the function factorial() that takes integer N as input parameter and returns a list of integers denoting the digits that make up the factorial of N.
Expected Time Complexity : O(N^2) Expected Auxilliary Space : O(1)
- Constraints:
1 ≤ N ≤ 1000
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
vector<int> factorial(int N){
vector<int>number;
number.push_back(1);
for(int i = 2;i<=N;i++){
multiply(i,number);
}
reverse(number.begin(),number.end());
return number;
}
void multiply(int n, vector<int>&number){
int carry = 0;
for(int i = 0;i<number.size();i++){
int num = n*number[i];
number[i] = (char)((num+carry)%10);
carry = (num+carry)/10;
}
while(carry){
number.push_back(carry%10);
carry /= 10;
}
}
};
int main() {
int t;
cin >> t;
while (t--) {
int N;
cin >> N;
Solution ob;
vector<int> result = ob.factorial(N);
for (int i = 0; i < result.size(); ++i){
cout<< result[i];
}
cout << endl;
}
return 0;
}Maximum Product Subarray
Given an array Arr[] that contains N integers (may be positive, negative or zero). Find the product of the maximum product subarray.
Example 1:
Input:
N = 5
Arr[] = {6, -3, -10, 0, 2}
Output: 180
Explanation: Subarray with maximum product is [6, -3, -10] which gives product as 180.
Example 2:
Input:
N = 6
Arr[] = {2, 3, 4, 5, -1, 0}
Output: 120
Explanation: Subarray with maximum product is [2, 3, 4, 5] which gives product as 120.
Your Task:
You don't need to read input or print anything. Your task is to complete the function maxProduct() which takes the array of integers arr and n as parameters and returns an integer denoting the answer.
Note: Use 64-bit integer data type to avoid overflow.
Expected Time Complexity: O(N) Expected Auxiliary Space: O(1)
- Constraints:
1 ≤ N ≤ 500
-10^2 ≤ Arri ≤ 10^2
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
// Function to find maximum product subarray
long long maxProduct(vector<int> arr, int n) {
long long minVal = arr[0];
long long maxVal = arr[0];
long long maxProduct = arr[0];
for(int i = 1;i<n;i++){
if(arr[i]<0)swap(maxVal,minVal);
maxVal = max((long long)arr[i], maxVal*arr[i]);
minVal = min((long long)arr[i], minVal*arr[i]);
maxProduct = max(maxProduct, maxVal);
}
return maxProduct;
}
};
int main() {
int t;
cin >> t;
while (t--) {
int n, i;
cin >> n;
vector<int> arr(n);
for (i = 0; i < n; i++) {
cin >> arr[i];
}
Solution ob;
auto ans = ob.maxProduct(arr, n);
cout << ans << "\n";
}
return 0;
}Longest consecutive subsequence
Given an array of positive integers. Find the length of the longest sub-sequence such that elements in the subsequence are consecutive integers, the consecutive numbers can be in any order.
Example 1:
Input:
N = 7
a[] = {2,6,1,9,4,5,3}
Output:
6
Explanation:
The consecutive numbers here are 1, 2, 3, 4, 5, 6. These 6 numbers form the longest consecutive subsquence.
Example 2:
Input:
N = 7
a[] = {1,9,3,10,4,20,2}
Output:
4
Explanation:
1, 2, 3, 4 is the longest consecutive subsequence.
Your Task:
You don't need to read input or print anything. Your task is to complete the function findLongestConseqSubseq() which takes the array arr[] and the size of the array as inputs and returns the length of the longest subsequence of consecutive integers.
Expected Time Complexity: O(N). Expected Auxiliary Space: O(N).
- Constraints:
1 <= N <= 10^5
0 <= a[i] <= 10^5
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
int findLongestConseqSubseq(int arr[], int N){
unordered_set<int>S;
int ans = 0;
for(int i = 0;i<N;i++){
S.insert(arr[i]);
}
for(int i = 0;i<N;i++){
if(S.find(arr[i] - 1)==S.end()){
int j = arr[i];
while(S.find(j) != S.end())j++;
ans = max(ans, j-arr[i]);
}
}
return ans;
}
};
int main()
{
int t,n,i,a[100001];
cin>>t;
while(t--)
{
cin>>n;
for(i=0;i<n;i++)
cin>>a[i];
Solution obj;
cout<<obj.findLongestConseqSubseq(a, n)<<endl;
}
return 0;
}Given an array of size n and a number k, find all elements that appear more than n/k times
Given an array of size n, find all elements in array that appear more than n/k times. For example, if the input arrays is {3, 1, 2, 2, 1, 2, 3, 3} and k is 4, then the output should be [2, 3]. Note that size of array is 8 (or n = 8), so we need to find all elements that appear more than 2 (or 8/4) times. There are two elements that appear more than two times, 2 and 3.
A simple method is to pick all elements one by one. For every picked element, count its occurrences by traversing the array, if count becomes more than n/k, then print the element. Time Complexity of this method would be O(n^2).
// C++ code to find elements whose
// frequency yis more than n/k
#include<bits/stdc++.h>
using namespace std;
void morethanNbyK(int arr[], int n, int k)
{
int x = n / k;
// unordered_map initialization
unordered_map<int, int> freq;
for(int i = 0; i < n; i++)
{
freq[arr[i]]++;
}
// Traversing the map
for(auto i : freq)
{
// Checking if value of a key-value pair
// is greater than x (where x=n/k)
if (i.second > x)
{
// Print the key of whose value
// is greater than x
cout << i.first << endl;
}
}
}
// Driver Code
int main()
{
int arr[] = { 1, 1, 2, 2, 3, 5,
4, 2, 2, 3, 1, 1, 1 };
int n = sizeof(arr) / sizeof(arr[0]);
int k = 4;
morethanNbyK(arr, n, k);
return 0;
}A better solution is to use sorting. First, sort all elements using a O(nLogn) algorithm. Once the array is sorted, we can find all required elements in a linear scan of array. So overall time complexity of this method is O(nLogn) + O(n) which is O(nLogn).
Following is an interesting O(nk) solution:
We can solve the above problem in O(nk) time using O(k-1) extra space. Note that there can never be more than k-1 elements in output.There are mainly three steps in this algorithm.
- Create a temporary array of size
(k-1)to store elements and their counts (The output elements are going to be among these k-1 elements). Following is structure of temporary array elements.
struct eleCount {
int eent;
int count;
};
struct eleCount temp[];
This step takes O(k) time.
-
Traverse through the input array and
update temp[](add/remove an element or increase/decrease count) for every traversed element. The array temp[] storespotential (k-1) candidatesat every step. This step takes O(nk) time. -
Iterate through
final (k-1) potential candidates(stored in temp[]). or every element, check if it actually has countmore than n/k. This step takesO(nk) time.
The main step is step 2, to maintain (k-1) potential candidates at every point.
The steps used in step 2 are like famous game: Tetris. We treat each number as a piece in Tetris, which falls down in our temporary array temp[]. Our task is to try to keep the same number stacked on the same column (count in temporary array is incremented).
// C++ code to find elements whose
// frequency yis more than n/k
#include<bits/stdc++.h>
using namespace std;
void morethanNbyK(int arr[], int n, int k)
{
int x = n / k;
// unordered_map initialization
unordered_map<int, int> freq;
for(int i = 0; i < n; i++)
{
freq[arr[i]]++;
}
// Traversing the map
for(auto i : freq)
{
// Checking if value of a key-value pair
// is greater than x (where x=n/k)
if (i.second > x)
{
// Print the key of whose value
// is greater than x
cout << i.first << endl;
}
}
}
int main()
{
int arr[] = { 1, 1, 2, 2, 3, 5, 4, 2, 2, 3, 1, 1, 1 };
int n = sizeof(arr) / sizeof(arr[0]);
int k = 4;
morethanNbyK(arr, n, k);
return 0;
}Consider k = 4, n = 9
Given array: 3 1 2 2 2 1 4 3 3
i = 0
3 _ _
temp[] has one element, 3 with count 1
i = 1
3 1 _
temp[] has two elements, 3 and 1 with
counts 1 and 1 respectively
i = 2
3 1 2
temp[] has three elements, 3, 1 and 2 with
counts as 1, 1 and 1 respectively.
i = 3
- - 2
3 1 2
temp[] has three elements, 3, 1 and 2 with
counts as 1, 1 and 2 respectively.
i = 4
- - 2
- - 2
3 1 2
temp[] has three elements, 3, 1 and 2 with
counts as 1, 1 and 3 respectively.
i = 5
- - 2
- 1 2
3 1 2
temp[] has three elements, 3, 1 and 2 with
counts as 1, 2 and 3 respectively.
Now the question arises, what to do when temp[] is full and we see a new element – we remove the bottom row from stacks of elements, i.e., we decrease count of every element by 1 in temp[]. We ignore the current element.
i = 6
- - 2
- 1 2
temp[] has two elements, 1 and 2 with
counts as 1 and 2 respectively.
i = 7
- 2
3 1 2
temp[] has three elements, 3, 1 and 2 with
counts as 1, 1 and 2 respectively.
i = 8
3 - 2
3 1 2
temp[] has three elements, 3, 1 and 2 with
counts as 2, 1 and 2 respectively.
Finally, we have at most k-1 numbers in temp[]. The elements in temp are {3, 1, 2}. Note that the counts in temp[] are useless now, the counts were needed only in step 2. Now we need to check whether the actual counts of elements in temp[] are more than n/k (9/4) or not. The elements 3 and 2 have counts more than 9/4. So we print 3 and 2.
Note that the algorithm doesn’t miss any output element. There can be two possibilities, many occurrences are together or spread across the array. If occurrences are together, then count will be high and won’t become 0. If occurrences are spread, then the element would come again in temp[]. Following is the implementation of the above algorithm.
// A C++ program to print elements with count more than n/k
#include <iostream>
using namespace std;
// A structure to store an element and its current count
struct eleCount {
int e; // Element
int c; // Count
};
// Prints elements with more
// than n/k occurrences in arr[]
// of size n. If there are no
// such elements, then it prints
// nothing.
void moreThanNdK(int arr[], int n, int k)
{
// k must be greater than
// 1 to get some output
if (k < 2)
return;
/* Step 1: Create a temporary
array (contains element
and count) of size k-1.
Initialize count of all
elements as 0 */
struct eleCount temp[k - 1];
for (int i = 0; i < k - 1; i++)
temp[i].c = 0;
/* Step 2: Process all
elements of input array */
for (int i = 0; i < n; i++)
{
int j;
/* If arr[i] is already present in
the element count array,
then increment its count
*/
for (j = 0; j < k - 1; j++)
{
if (temp[j].e == arr[i])
{
temp[j].c += 1;
break;
}
}
/* If arr[i] is not present in temp[] */
if (j == k - 1) {
int l;
/* If there is position available
in temp[], then place arr[i] in
the first available position and
set count as 1*/
for (l = 0; l < k - 1; l++)
{
if (temp[l].c == 0)
{
temp[l].e = arr[i];
temp[l].c = 1;
break;
}
}
/* If all the position in the
temp[] are filled, then decrease
count of every element by 1 */
if (l == k - 1)
for (l = 0; l < k-1; l++)
temp[l].c -= 1;
}
}
/*Step 3: Check actual counts of
* potential candidates in temp[]*/
for (int i = 0; i < k - 1; i++)
{
// Calculate actual count of elements
int ac = 0; // actual count
for (int j = 0; j < n; j++)
if (arr[j] == temp[i].e)
ac++;
// If actual count is more than n/k,
// then print it
if (ac > n / k)
cout << "Number:" << temp[i].e
<< " Count:" << ac << endl;
}
}
/* Driver code */
int main()
{
cout << "First Test\n";
int arr1[] = { 4, 5, 6, 7, 8, 4, 4 };
int size = sizeof(arr1) / sizeof(arr1[0]);
int k = 3;
moreThanNdK(arr1, size, k);
cout << "\nSecond Test\n";
int arr2[] = { 4, 2, 2, 7 };
size = sizeof(arr2) / sizeof(arr2[0]);
k = 3;
moreThanNdK(arr2, size, k);
cout << "\nThird Test\n";
int arr3[] = { 2, 7, 2 };
size = sizeof(arr3) / sizeof(arr3[0]);
k = 2;
moreThanNdK(arr3, size, k);
cout << "\nFourth Test\n";
int arr4[] = { 2, 3, 3, 2 };
size = sizeof(arr4) / sizeof(arr4[0]);
k = 3;
moreThanNdK(arr4, size, k);
return 0;
}Output :
First Test Number:4 Count:3 Second Test Number:2 Count:2 Third Test Number:2 Count:2 Fourth Test Number:2 Count:2 Number:3 Count:2
Time Complexity: O(nk) Auxiliary Space: O(k)
Generally asked variations of this problem are, find all elements that appear n/3 times or n/4 times in O(n) time complexity and O(1) extra space.
Hashing can also be an efficient solution. With a good hash function, we can solve the above problem in O(n) time on average. Extra space required hashing would be higher than O(k). Also, hashing cannot be used to solve the above variations with O(1) extra space.
Below is the implementation of the above idea:
// C++ code to find elements whose
// frequency yis more than n/k
#include<bits/stdc++.h>
using namespace std;
void morethanNbyK(int arr[], int n, int k)
{
int x = n / k;
// unordered_map initialization
unordered_map<int, int> freq;
for(int i = 0; i < n; i++)
{
freq[arr[i]]++;
}
// Traversing the map
for(auto i : freq)
{
// Checking if value of a key-value pair
// is greater than x (where x=n/k)
if (i.second > x)
{
// Print the key of whose value
// is greater than x
cout << i.first << endl;
}
}
}
// Driver Code
int main()
{
int arr[] = { 1, 1, 2, 2, 3, 5,
4, 2, 2, 3, 1, 1, 1 };
int n = sizeof(arr) / sizeof(arr[0]);
int k = 4;
morethanNbyK(arr, n, k);
return 0;
}Output :
1 2
- Count the frequencies of every element using
Counter()function. - Traverse the frequency array and print all the elements which occur at
more than n/ktimes.
Below is the implementation:
// C++ implementation
#include <bits/stdc++.h>
using namespace std;
// Function to find the number of array
// elements with frequency more than n/k times
void printElements(int arr[], int n, int k)
{
// Calculating n/k
int x = n / k;
// Counting frequency of every
// element using Counter
map<int, int> mp;
for (int i = 0; i < n; i++)
mp[arr[i]] += 1;
// Traverse the map and print all
// the elements with occurrence
// more than n/k times
for (int it = 0; it < mp.size(); it++) {
if (mp[it] > x)
cout << (it) << endl;
}
}
// Driver code
int main()
{
int arr[] = { 1, 1, 2, 2, 3, 5, 4, 2, 2, 3, 1, 1, 1 };
int n = sizeof(arr) / sizeof(arr[0]);
int k = 4;
printElements(arr, n, k);
}Output:
1 2
Time Complexity: O(N) Auxiliary Space: O(N)
Maximum profit by buying and selling a share at most twice
In daily share trading, a buyer buys shares in the morning and sells them on the same day. If the trader is allowed to make at most 2 transactions in a day, whereas the second transaction can only start after the first one is complete (Buy->sell->Buy->sell). Given stock prices throughout the day, find out the maximum profit that a share trader could have made.
Examples:
Input: price[] = {10, 22, 5, 75, 65, 80}
Output: 87
Trader earns 87 as sum of 12, 75
Buy at 10, sell at 22,
Buy at 5 and sell at 80
Input: price[] = {2, 30, 15, 10, 8, 25, 80}
Output: 100
Trader earns 100 as sum of 28 and 72
Buy at price 2, sell at 30, buy at 8 and sell at 80
Input: price[] = {100, 30, 15, 10, 8, 25, 80};
Output: 72
Buy at price 8 and sell at 80.
Input: price[] = {90, 80, 70, 60, 50}
Output: 0
Not possible to earn.
A Simple Solution is to consider every index ‘i’ and do the following.
Max profit with at most two transactions =
MAX {max profit with one transaction and subarray price[0..i] +
max profit with one transaction and subarray price[i+1..n-1] }
i varies from 0 to n-1.
We can do this O(n) using the following Efficient Solution. The idea is to store the maximum possible profit of every subarray and solve the problem in the following two phases.
- Create a table
profit[0..n-1]and initialize all values in it0. - Traverse price[] from right to left and update profit[i] such that profit[i] stores
maximum profit achievablefrom one transaction in subarrayprice[i..n-1] - Traverse price[] from left to right and update profit[i] such that profit[i] stores
maximum profit such that profit[i]containsmaximum achievable profitfromtwotransactions in subarray price[0..i]. - Return
profit[n-1]
To do step 2, we need to keep track of the maximum price from right to left side, and to do step 3, we need to keep track of the minimum price from left to right.
To save space, in the third step, we use the same array for both purposes, maximum with 1 transaction and maximum with 2 transactions. After iteration i, the array profit[0..i] contains the maximum profit with 2 transactions, and profit[i+1..n-1] contains profit with two transactions.
Below are the implementations of the above idea.
// C++ program to find maximum
// possible profit with at most
// two transactions
#include <bits/stdc++.h>
using namespace std;
// Returns maximum profit with
// two transactions on a given
// list of stock prices, price[0..n-1]
int maxProfit(int price[], int n)
{
// Create profit array and
// initialize it as 0
int* profit = new int[n];
for (int i = 0; i < n; i++)
profit[i] = 0;
/* Get the maximum profit with
only one transaction
allowed. After this loop,
profit[i] contains maximum
profit from price[i..n-1]
using at most one trans. */
int max_price = price[n - 1];
for (int i = n - 2; i >= 0; i--) {
// max_price has maximum
// of price[i..n-1]
if (price[i] > max_price)
max_price = price[i];
// we can get profit[i] by taking maximum of:
// a) previous maximum, i.e., profit[i+1]
// b) profit by buying at price[i] and selling at
// max_price
profit[i]
= max(profit[i + 1], max_price - price[i]);
}
/* Get the maximum profit with two transactions allowed
After this loop, profit[n-1] contains the result */
int min_price = price[0];
for (int i = 1; i < n; i++) {
// min_price is minimum price in price[0..i]
if (price[i] < min_price)
min_price = price[i];
// Maximum profit is maximum of:
// a) previous maximum, i.e., profit[i-1]
// b) (Buy, Sell) at (min_price, price[i]) and add
// profit of other trans. stored in profit[i]
profit[i] = max(profit[i - 1],
profit[i] + (price[i] - min_price));
}
int result = profit[n - 1];
delete[] profit; // To avoid memory leak
return result;
}
// Driver code
int main()
{
int price[] = { 2, 30, 15, 10, 8, 25, 80 };
int n = sizeof(price) / sizeof(price[0]);
cout << "Maximum Profit = " << maxProfit(price, n);
return 0;
}Output:
Maximum Profit = 100
The time complexity of the above solution is O(n).
Algorithmic Paradigm: Dynamic Programming
Initialize four variables for taking care of the first buy, first sell, second buy, second sell. Set first buy and second buy as INT_MIN and first and second sell as 0. This is to ensure to get profit from transactions. Iterate through the array and return the second sell as it will store maximum profit.
#include <iostream>
#include<climits>
using namespace std;
int maxtwobuysell(int arr[],int size) {
int first_buy = INT_MIN;
int first_sell = 0;
int second_buy = INT_MIN;
int second_sell = 0;
for(int i=0;i<size;i++) {
first_buy = max(first_buy,-arr[i]);//we set prices to negative, so the calculation of profit will be convenient
first_sell = max(first_sell,first_buy+arr[i]);
second_buy = max(second_buy,first_sell-arr[i]);//we can buy the second only after first is sold
second_sell = max(second_sell,second_buy+arr[i]);
}
return second_sell;
}
int main() {
int arr[] = {2, 30, 15, 10, 8, 25, 80};
int size = sizeof(arr)/sizeof(arr[0]);
cout<<maxtwobuysell(arr,size);
return 0;
}Output:
100
Time Complexity: O(N) Auxiliary Space: O(1)
Find whether an array is a subset of another array
Given two arrays: a1[0..n-1] of size n and a2[0..m-1] of size m. Task is to check whether a2[] is a subset of a1[] or not. Both the arrays can be sorted or unsorted.
Example 1:
Input:
a1[] = {11, 1, 13, 21, 3, 7}
a2[] = {11, 3, 7, 1}
Output:
Yes
Explanation: a2[] is a subset of a1[]
Example 2:
Input:
a1[] = {1, 2, 3, 4, 5, 6}
a2[] = {1, 2, 4}
Output:
Yes
Explanation: a2[] is a subset of a1[]
Example 3:
Input:
a1[] = {10, 5, 2, 23, 19}
a2[] = {19, 5, 3}
Output:
No
Explanation: a2[] is not a subset of a1[]
Your Task:
You don't need to read input or print anything. Your task is to complete the function isSubset() which takes the array a1[], a2[], its size n and m as inputs and return "Yes" if arr2 is subset of arr1 else return "No" if arr2 is not subset of arr1.
Expected Time Complexity: O(n) Expected Auxiliary Space: O(n)
- Constraints:
1 <= n,m <= 10^5
1 <= a1[i], a2[j] <= 10^5
#include <bits/stdc++.h>
using namespace std;
string isSubset(int a1[], int a2[], int n, int m) ;
int main() {
int t;
cin >> t;
while (t--) {
int n, m;
cin >> n >> m;
int a1[n], a2[m];
for (int i = 0; i < n; i++) {
cin >> a1[i];
}
for (int i = 0; i < m; i++) {
cin >> a2[i];
}
cout << isSubset(a1, a2, n, m) << endl;
}
return 0;
}
string isSubset(int a1[], int a2[], int n, int m) {
unordered_map<int, int>um, um2;
for(int i = 0;i<n;i++)um[a1[i]]++;
for(int i = 0;i<m;i++)um2[a2[i]]++;
int count = 0;
for(auto it = um2.begin(); it != um2.end(); it++){
if(um[it->first] >= it->second){
count++;
}
}
if (count == m)return "Yes";
else return "No";
}Find the triplet that sum to a given value
Given an array arr of size n and an integer X. Find if there's a triplet in the array which sums up to the given integer X.
Example 1:
Input:
n = 6, X = 13
arr[] = [1 4 45 6 10 8]
Output:
1
Explanation: The triplet {1, 4, 8} in the array sums up to 13.
Example 2:
Input:
n = 5, X = 10
arr[] = [1 2 4 3 6]
Output:
1
Explanation: The triplet {1, 3, 6} in the array sums up to 10.
Your Task:
You don't need to read input or print anything. Your task is to complete the function find3Numbers() which takes the array arr[], the size of the array (n) and the sum (X) as inputs and returns True if there exists a triplet in the array arr[] which sums up to X and False otherwise.
Expected Time Complexity: O(n^2) Expected Auxiliary Space: O(1)
- Constraints:
1 ≤ n ≤ 10^3
1 ≤ A[i] ≤ 10^5
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
bool find3Numbers(int A[], int n, int X){
sort(A,A+n);
int l, r;
for(int i = 0; i<n-2; i++){
l = i+1;
r = n-1;
while(l<r){
if(A[i]+A[l]+A[r] == X)return -1;
else if(A[i]+A[l]+A[r]<X)l++;
else r--;
}
}
return 0;
}
};
int main()
{
int T;
cin>>T;
while(T--)
{
int n,X;
cin>>n>>X;
int i,A[n];
for(i=0;i<n;i++)
cin>>A[i];
Solution ob;
cout << ob.find3Numbers(A, n, X) << endl;
}
}Trapping Rain water problem
Given an array arr[] of N non-negative integers representing the height of blocks. If width of each block is 1, compute how much water can be trapped between the blocks during the rainy season.
Example 1:
Input:
N = 6
arr[] = {3,0,0,2,0,4}
Output:
10
Explanation:
Example 2:
Input:
N = 4
arr[] = {7,4,0,9}
Output:
10
Explanation: Water trapped by above block of height 4 is 3 units and above block of height 0 is 7 units. So, the total unit of water trapped is 10 units.
Example 3:
Input:
N = 3
arr[] = {6,9,9}
Output:
0
Explanation: No water will be trapped.
Your Task:
You don't need to read input or print anything. The task is to complete the function trappingWater() which takes arr[] and N as input parameters and returns the total amount of water that can be trapped.
Expected Time Complexity: O(N) Expected Auxiliary Space: O(N)
- Constraints:
3 < N < 10^6
0 < Ai < 10^8
#include<bits/stdc++.h>
using namespace std;
class Solution{
// Function to find the trapped water between the blocks.
public:
long long trappingWater(int arr[], int n){
vector<int>left(n, 0);
vector<int>right(n, 0);
long long water = 0;
left[0] = arr[0];
for(int i = 1;i<n;i++){
left[i] = max(left[i-1],arr[i]);
}
right[n-1] = arr[n-1];
for(int i = n-2;i>=0;i--){
right[i] = max(right[i+1],arr[i]);
}
for(int i = 0;i<n;i++){
water += max(0,min(left[i] ,right[i]) - arr[i]);
}
return water;
}
};
int main(){
int t;
//testcases
cin >> t;
while(t--){
int n;
//size of array
cin >> n;
int a[n];
//adding elements to the array
for(int i =0;i<n;i++){
cin >> a[i];
}
Solution obj;
//calling trappingWater() function
cout << obj.trappingWater(a, n) << endl;
}
return 0;
}Chocolate Distribution Problem
Given an array A[ ] of positive integers of size N, where each value represents the number of chocolates in a packet. Each packet can have a variable number of chocolates. There are M students, the task is to distribute chocolate packets among M students such that :
- Each student gets exactly
onepacket. - The difference between maximum number of chocolates given to a student and minimum number of chocolates given to a student is
minimum.
Example 1:
Input:
N = 8, M = 5
A = {3, 4, 1, 9, 56, 7, 9, 12}
Output: 6
Explanation: The minimum difference between maximum chocolates and minimum chocolates is 9 - 3 = 6 by choosing following M packets :
{3, 4, 9, 7, 9}.
Example 2:
Input:
N = 7, M = 3
A = {7, 3, 2, 4, 9, 12, 56}
Output: 2
Explanation: The minimum difference between maximum chocolates and minimum chocolates is 4 - 2 = 2 by choosing following M packets :
{3, 2, 4}.
Your Task:
You don't need to take any input or print anything. Your task is to complete the function findMinDiff() which takes array A[ ], N and M as input parameters and returns the minimum possible difference between maximum number of chocolates given to a student and minimum number of chocolates given to a student.
Expected Time Complexity: O(N*Log(N)) Expected Auxiliary Space: O(1)
- Constraints:
1 ≤ T ≤ 100
1 ≤ N ≤ 10^5
1 ≤ Ai ≤ 10^9
1 ≤ M ≤ N
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
long long findMinDiff(vector<long long> a, long long n, long long m){
sort(a.begin(),a.end());
long long start = 0, end = 0;
long long mind = LONG_LONG_MAX;
for(long long i = 0;i+m-1<n;i++){
long long diff = a[i+m-1]-a[i];
if(mind>diff){
mind = diff;
start = i;
end = i+m-1;
}
}
return a[end]-a[start];
}
};
int main() {
long long t;
cin>>t;
while(t--)
{
long long n;
cin>>n;
vector<long long> a;
long long x;
for(long long i=0;i<n;i++)
{
cin>>x;
a.push_back(x);
}
long long m;
cin>>m;
Solution ob;
cout<<ob.findMinDiff(a,n,m)<<endl;
}
return 0;
}Smallest Subarray with sum greater than a given value
Given an array of integers (A[]) and a number x, find the smallest subarray with sum greater than the given value.
Note: The answer always exists. It is guaranteed that x doesn't exceed the summation of a[i] (from 1 to N).
Example 1:
Input:
A[] = {1, 4, 45, 6, 0, 19}
x = 51
Output: 3
Explanation: Minimum length subarray is
{4, 45, 6}
Example 2:
Input:
A[] = {1, 10, 5, 2, 7}
x = 9
Output: 1
Explanation: Minimum length subarray is {10}
Your Task:
You don't need to read input or print anything. Your task is to complete the function smallestSubWithSum() which takes the array A[], its size N and an integer X as inputs and returns the required ouput.
Expected Time Complexity: O(N) Expected Auxiliary Space: O(1)
- Constraints:
1 ≤ N, x ≤ 10^5
1 ≤ A[] ≤ 10^4
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
int smallestSubWithSum(int arr[], int n, int x)
{
// Initialize current sum and minimum length
int curr_sum = 0, min_len = n+1;
// Initialize starting and ending indexes
int start = 0, end = 0;
while (end < n)
{
// Keep adding array elements while current sum
// is smaller than x
while (curr_sum <= x && end < n)
curr_sum += arr[end++];
// If current sum becomes greater than x.
while (curr_sum > x && start < n)
{
// Update minimum length if needed
if (end - start < min_len)
min_len = end - start;
curr_sum -= arr[start++];
}
}
if(min_len>n)
return 0;
return min_len;
}
};
int main() {
// your code goes here
int t;
cin>>t;
while(t--)
{
int n,x;
cin>>n>>x;
int a[n];
for(int i=0;i<n;i++)
cin>>a[i];
Solution obj;
cout<<obj.smallestSubWithSum(a,n,x)<<endl;
}
return 0;
}Three way partitioning of an array around a given value
Given an array of size n and a range [a, b]. The task is to partition the array around the range such that array is divided into three parts.
- All elements smaller than
acome first. - All elements in range
atobcome next. - All elements greater than
bappear in the end.
The individual elements of three sets can appear in any order. You are required to return the modified array.
Example 1:
Input:
n = 5
A[] = {1, 2, 3, 3, 4}
[a, b] = [1, 2]
Output: 1
Explanation: One possible arrangement is:
{1, 2, 3, 3, 4}. If you return a valid arrangement, output will be 1.
Example 2:
Input:
n = 3
A[] = {1, 2, 3}
[a, b] = [1, 3]
Output: 1
Explanation: One possible arrangement is:
{1, 2, 3}. If you return a valid arrangement, output will be 1.
Your Task:
You dont need to read input or print anything. The task is to complete the function threeWayPartition() which takes the array[], a and b as input parameters and modifies the array in-place according to the given conditions.
Note: The generated output is 1 if you modify the given array successfully.
Expected Time Complexity: O(n) Expected Auxiliary Space: O(1)
- Constraints:
1 <= n <= 10^6
1 <= A[i] <= 10^6
#include <bits/stdc++.h>
#include <unordered_map>
using namespace std;
class Solution{
public:
void threeWayPartition(vector<int>& array,int a, int b){
int start = 0, end = array.size()-1;
for(int i = 0;i<=end;){
if(array[i]<a)swap(&array[i++], &array[start++]);
else if(array[i]>b)swap(&array[i], &array[end--]);
else i++;
}
}
void swap(int *xp, int *yp){
int temp = *xp;
*xp = *yp;
*yp = temp;
}
};
int main() {
int t;
cin>>t;
while(t--)
{
int N;
cin>>N;
vector<int> array(N);
unordered_map<int,int> ump;
for(int i=0;i<N;i++){
cin>>array[i];
ump[array[i]]++;
}
int a,b;
cin>>a>>b;
vector<int> original = array;
int k1=0,k2=0,k3=0;
int kk1=0;int kk2=0;int kk3=0;
for(int i=0; i<N; i++)
{
if(original[i]>b)
k3++;
else if(original[i]<=b and original[i]>=a)
k2++;
else if(original[i]<b)
k1++;
}
Solution ob;
ob.threeWayPartition(array,a,b);
for(int i=0;i<k1;i++)
{
if(array[i]<b)
kk1++;
}
for(int i=k1;i<k1+k2;i++)
{
if(array[i]<=b and array[i]>=a)
kk2++;
}
for(int i=k1+k2;i<k1+k2+k3;i++)
{
if(array[i]>b)
kk3++;
}
bool ok = 0;
if(k1==kk1 and k2 ==kk2 and k3 == kk3)
ok = 1;
for(int i=0;i<array.size();i++)
ump[array[i]]--;
for(int i=0;i<array.size();i++)
if(ump[array[i]]!=0)
ok=0;
if(ok)
cout<<1<<endl;
else
cout<<0<<endl;
}
return 0;
}Minimum swaps required bring elements less equal K together
Given an array arr of n positive integers and a number k. One can apply a swap operation on the array any number of times, i.e choose any two index i and j (i < j) and swap arr[i] , arr[j] . Find the minimum number of swaps required to bring all the numbers less than or equal to k together, i.e. make them a contiguous subarray.
Example 1:
Input :
arr[ ] = {2, 1, 5, 6, 3}
K = 3
Output :
1
Explanation: To bring elements 2, 1, 3 together, swap index 2 with 4 (0-based indexing), i.e. element arr[2] = 5 with arr[4] = 3 such that final array will be-
arr[] = {2, 1, 3, 6, 5}
Example 2:
Input :
arr[ ] = {2, 7, 9, 5, 8, 7, 4}
K = 6
Output :
2
Explanation: To bring elements 2, 5, 4 together, swap index 0 with 2 (0-based indexing) and index 4 with 6 (0-based indexing) such that final array will be-
arr[] = {9, 7, 2, 5, 4, 7, 8}
Your Task:
This is a function problem. The input is already taken care of by the driver code. You only need to complete the function minSwap() that takes an array (arr), sizeOfArray (n), an integer K, and return the minimum swaps required. The driver code takes care of the printing.
Expected Time Complexity: O(N). Expected Auxiliary Space: O(1).
- Constraints:
1 ≤ N ≤ 10^5
1 ≤ Arri, K ≤10^7
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
int minSwap(int arr[], int n, int k){
int count = 0;
for(int i = 0;i<n;i++){
if(arr[i] <= k)count++;
}
int bad = 0;
for(int i = 0;i<count;i++){
if(arr[i]>k)bad++;
}
int ans = bad;
for(int i = 0, j = count; j<n; i++,j++){
if(arr[i]>k)--bad;
if(arr[j]>k)++bad;
ans = min(ans,bad);
}
return ans;
}
};
int main() {
int t,n,k;
cin>>t;
while(t--)
{
cin>>n;
int arr[n];
for(int i=0;i<n;i++)
cin>>arr[i];
cin>>k;
Solution ob;
cout << ob.minSwap(arr, n, k) << "\n";
}
return 0;
}Palindromic Array
Given a Integer array A[] of n elements. Your task is to complete the function PalinArray. Which will return 1 if all the elements of the Array are palindrome otherwise it will return 0.
Example:
Input:
2
5
111 222 333 444 555
3
121 131 20
Output:
1
0
Explanation:
For First test case.
n=5;
A[0] = 111 //which is a palindrome number.
A[1] = 222 //which is a palindrome number.
A[2] = 333 //which is a palindrome number.
A[3] = 444 //which is a palindrome number.
A[4] = 555 //which is a palindrome number.
As all numbers are palindrome so This will return 1.
- Constraints:
1 <=T<= 50
1 <=n<= 20
1 <=A[]<= 10000
#include<iostream>
#include<string.h>
using namespace std;
class Solution {
public:
bool isPalindrome(int x){
int copy = x;
int rem = 0;
int rev = 0;
while(copy!=0){
rem = copy%10;
rev = rev*10+rem;
copy/=10;
}
if(x!=rev)return false;
return true;
}
int PalinArray(int a[], int n){
for(int i = 0;i<n;i++){
if(!isPalindrome(a[i]))return 0;
}
return 1;
}
};
int main()
{
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
int a[n];
for(int i = 0; i < n; i++)
cin>>a[i];
Solution obj;
cout<<obj.PalinArray(a,n)<<endl;
}
}Find minimum number of merge operations to make an array palindrome
Given an array of positive integers. We need to make the given array a ‘Palindrome’. The only allowed operation is”merging” (of two adjacent elements). Merging two adjacent elements means replacing them with their sum. The task is to find the minimum number of merge operations required to make the given array a ‘Palindrome’.
To make any array a palindrome, we can simply apply merge operation n-1 times where n is the size of the array (because a single-element array is always palindromic, similar to single-character string). In that case, the size of array will be reduced to 1. But in this problem, we are asked to do it in the minimum number of operations.
Example :
Input : arr[] = {15, 4, 15}
Output : 0
Array is already a palindrome. So we
do not need any merge operation.
Input : arr[] = {1, 4, 5, 1}
Output : 1
We can make given array palindrome with
minimum one merging (merging 4 and 5 to
make 9)
Input : arr[] = {11, 14, 15, 99}
Output : 3
We need to merge all elements to make
a palindrome.
The expected time complexity is O(n).
Let f(i, j) be minimum merging operations to make subarray arr[i..j] a palindrome. If i == j answer is 0. We start i from 0 and j from n-1.
- If
arr[i] == arr[j], then there is no need to do any merging operations at indexior indexj. Our answer in this case will bef(i+1, j-1). - Else, we need to do merging operations. Following cases arise.
- If
arr[i] > arr[j], then we should do merging operation at indexj. We merge indexj-1andj, and updatearr[j-1] = arr[j-1] + arr[j]. Our answer in this case will be1 + f(i, j-1). - For the case when
arr[i] < arr[j], updatearr[i+1] = arr[i+1] + arr[i]. Our answer in this case will be1 + f(i+1, j).
- If
- Our answer will be
f(0, n-1), wherenis the size of arrayarr[].
Therefore this problem can be solved iteratively using two pointers (first pointer pointing to start of the array and second pointer pointing to the last element of the array) method and keeping count of total merging operations done till now.
Below is an implementation of the above idea.
// C++ program to find number of operations
// to make an array palindrome
#include <bits/stdc++.h>
using namespace std;
// Returns minimum number of count operations
// required to make arr[] palindrome
int findMinOps(int arr[], int n)
{
int ans = 0; // Initialize result
// Start from two corners
for (int i=0,j=n-1; i<=j;)
{
// If corner elements are same,
// problem reduces arr[i+1..j-1]
if (arr[i] == arr[j])
{
i++;
j--;
}
// If left element is greater, then
// we merge right two elements
else if (arr[i] > arr[j])
{
// need to merge from tail.
j--;
arr[j] += arr[j+1] ;
ans++;
}
// Else we merge left two elements
else
{
i++;
arr[i] += arr[i-1];
ans++;
}
}
return ans;
}
int main()
{
int arr[] = {1, 4, 5, 9, 1};
int n = sizeof(arr)/sizeof(arr[0]);
cout << "Count of minimum operations is "
<< findMinOps(arr, n) << endl;
return 0;
}Output :
Count of minimum operations is 1
The time complexity for the given program is: O(n)
Median of two sorted arrays of same size
There are 2 sorted arrays A and B of size n each. Write an algorithm to find the median of the array obtained after merging the above 2 arrays(i.e. array of length 2n). The complexity should be O(log(n)).
Note: Since the size of the set for which we are looking for the median is even (2n), we need to take the average of the middle two numbers and return the floor of the average.
Use the merge procedure of merge sort. Keep track of count while comparing elements of two arrays. If count becomes n(For 2n elements), we have reached the median. Take the average of the elements at indexes n-1 and n in the merged array.
See the below implementation.
// A Simple Merge based O(n)
// solution to find median of
// two sorted arrays
#include <bits/stdc++.h>
using namespace std;
/* This function returns
median of ar1[] and ar2[].
Assumptions in this function:
Both ar1[] and ar2[]
are sorted arrays
Both have n elements */
int getMedian(int ar1[],
int ar2[], int n)
{
int i = 0; /* Current index of
i/p array ar1[] */
int j = 0; /* Current index of
i/p array ar2[] */
int count;
int m1 = -1, m2 = -1;
/* Since there are 2n elements,
median will be average of elements
at index n-1 and n in the array
obtained after merging ar1 and ar2 */
for (count = 0; count <= n; count++)
{
/* Below is to handle case where
all elements of ar1[] are
smaller than smallest(or first)
element of ar2[]*/
if (i == n)
{
m1 = m2;
m2 = ar2[0];
break;
}
/*Below is to handle case where
all elements of ar2[] are
smaller than smallest(or first)
element of ar1[]*/
else if (j == n)
{
m1 = m2;
m2 = ar1[0];
break;
}
/* equals sign because if two
arrays have some common elements */
if (ar1[i] <= ar2[j])
{
/* Store the prev median */
m1 = m2;
m2 = ar1[i];
i++;
}
else
{
/* Store the prev median */
m1 = m2;
m2 = ar2[j];
j++;
}
}
return (m1 + m2)/2;
}
int main()
{
int ar1[] = {1, 12, 15, 26, 38};
int ar2[] = {2, 13, 17, 30, 45};
int n1 = sizeof(ar1) / sizeof(ar1[0]);
int n2 = sizeof(ar2) / sizeof(ar2[0]);
if (n1 == n2)
cout << "Median is "
<< getMedian(ar1, ar2, n1) ;
else
cout << "Doesn't work for arrays"
<< " of unequal size" ;
getchar();
return 0;
}Output :
Median is 16
Time Complexity : O(n) Auxiliary Space: O(1)
This method works by first getting medians of the two sorted arrays and then comparing them.
Let ar1 and ar2 be the input arrays.
Algorithm :
1) Calculate the medians m1 and m2 of the input arrays ar1[]
and ar2[] respectively.
2) If m1 and m2 both are equal then we are done.
return m1 (or m2)
3) If m1 is greater than m2, then median is present in one
of the below two subarrays.
a) From first element of ar1 to m1 (ar1[0...|_n/2_|])
b) From m2 to last element of ar2 (ar2[|_n/2_|...n-1])
4) If m2 is greater than m1, then median is present in one
of the below two subarrays.
a) From m1 to last element of ar1 (ar1[|_n/2_|...n-1])
b) From first element of ar2 to m2 (ar2[0...|_n/2_|])
5) Repeat the above process until size of both the subarrays
becomes 2.
6) If size of the two arrays is 2 then use below formula to get
the median.
Median = (max(ar1[0], ar2[0]) + min(ar1[1], ar2[1]))/2
Examples:
ar1[] = {1, 12, 15, 26, 38}
ar2[] = {2, 13, 17, 30, 45}
For above two arrays m1 = 15 and m2 = 17
For the above ar1[] and ar2[], m1 is smaller than m2. So median is present in one of the following two subarrays.
[15, 26, 38] and [2, 13, 17]
Let us repeat the process for above two subarrays:
m1 = 26 m2 = 13.
m1 is greater than m2. So the subarrays become
[15, 26] and [13, 17]
Now size is 2, so median = (max(ar1[0], ar2[0]) + min(ar1[1], ar2[1]))/2
= (max(15, 13) + min(26, 17))/2
= (15 + 17)/2
= 16
// A divide and conquer based
// efficient solution to find
// median of two sorted arrays
// of same size.
#include<bits/stdc++.h>
using namespace std;
/* to get median of a
sorted array */
int median(int [], int);
/* This function returns median
of ar1[] and ar2[].
Assumptions in this function:
Both ar1[] and ar2[] are
sorted arrays
Both have n elements */
int getMedian(int ar1[],
int ar2[], int n)
{
/* return -1 for
invalid input */
if (n <= 0)
return -1;
if (n == 1)
return (ar1[0] +
ar2[0]) / 2;
if (n == 2)
return (max(ar1[0], ar2[0]) +
min(ar1[1], ar2[1])) / 2;
/* get the median of
the first array */
int m1 = median(ar1, n);
/* get the median of
the second array */
int m2 = median(ar2, n);
/* If medians are equal then
return either m1 or m2 */
if (m1 == m2)
return m1;
/* if m1 < m2 then median must
exist in ar1[m1....] and
ar2[....m2] */
if (m1 < m2)
{
if (n % 2 == 0)
return getMedian(ar1 + n / 2 - 1,
ar2, n - n / 2 + 1);
return getMedian(ar1 + n / 2,
ar2, n - n / 2);
}
/* if m1 > m2 then median must
exist in ar1[....m1] and
ar2[m2...] */
if (n % 2 == 0)
return getMedian(ar2 + n / 2 - 1,
ar1, n - n / 2 + 1);
return getMedian(ar2 + n / 2,
ar1, n - n / 2);
}
/* Function to get median
of a sorted array */
int median(int arr[], int n)
{
if (n % 2 == 0)
return (arr[n / 2] +
arr[n / 2 - 1]) / 2;
else
return arr[n / 2];
}
int main()
{
int ar1[] = {1, 2, 3, 6};
int ar2[] = {4, 6, 8, 10};
int n1 = sizeof(ar1) /
sizeof(ar1[0]);
int n2 = sizeof(ar2) /
sizeof(ar2[0]);
if (n1 == n2)
cout << "Median is "
<< getMedian(ar1, ar2, n1);
else
cout << "Doesn't work for arrays "
<< "of unequal size";
return 0;
}Output :
Median is 5
Time Complexity : O(logn) Auxiliary Space: O(1) Algorithmic Paradigm: Divide and Conquer
This method works by taking the union of two arrays without extra space and then sorting them.
Algorithm :
1) Take the union of the input arrays ar1[] and ar2[]. 2) Sort ar1[] and ar2[] respectively. 3) The median will be the last element of ar1[] + the first element of ar2[] divided by 2. [(ar1[n-1] + ar2[0])/2].
Implementation :
// CPP program for the above approach
#include <bits/stdc++.h>
using namespace std;
/* This function returns
median of ar1[] and ar2[].
Assumptions in this function:
Both ar1[] and ar2[]
are sorted arrays
Both have n elements */
int getMedian(int ar1[], int ar2[], int n)
{
int j = 0;
int i = n - 1;
while (ar1[i] > ar2[j] && j < n && i > -1)
swap(ar1[i--], ar2[j++]);
sort(ar1, ar1 + n);
sort(ar2, ar2 + n);
return (ar1[n - 1] + ar2[0]) / 2;
}
// Driver Code
int main()
{
int ar1[] = { 1, 12, 15, 26, 38 };
int ar2[] = { 2, 13, 17, 30, 45 };
int n1 = sizeof(ar1) / sizeof(ar1[0]);
int n2 = sizeof(ar2) / sizeof(ar2[0]);
if (n1 == n2)
cout << "Median is " << getMedian(ar1, ar2, n1);
else
cout << "Doesn't work for arrays"
<< " of unequal size";
getchar();
return 0;
}Output:
Median is 16
Time Complexity: O(nlogn) Auxiliary Space: O(1)
Median of two sorted arrays of different sizes
Given two sorted arrays, a[] and b[], the task is to find the median of these sorted arrays, in O(log n + log m) time complexity, when n is the number of elements in the first array, and m is the number of elements in the second array.
Example:
Input: ar1[] = {-5, 3, 6, 12, 15}
ar2[] = {-12, -10, -6, -3, 4, 10}
Output : The median is 3.
Explanation : The merged array is :
ar3[] = {-12, -10, -6, -5 , -3,
3, 4, 6, 10, 12, 15},
So the median of the merged array is 3
Input: ar1[] = {2, 3, 5, 8}
ar2[] = {10, 12, 14, 16, 18, 20}
Output : The median is 11.
Explanation : The merged array is :
ar3[] = {2, 3, 5, 8, 10, 12, 14, 16, 18, 20}
if the number of the elements are even,
so there are two middle elements,
take the average between the two :
(10 + 12) / 2 = 11.
Algorithm:
- Given two arrays are sorted. So they can be merged in O(m+n) time. Create a variable count to have a count of elements in the output array.
- If the value of (m+n) is odd then there is only one median else the median is the average of elements at index (m+n)/2 and ((m+n)/2 – 1).
- To merge the both arrays, keep two indices i and j initially assigned to 0. Compare the ith index of 1st array and jth index of second, increase the index of the smallest element and increase the count.
- Store (m+n)/2 and (m+n)/2-1 in two variables (In the below C++ code, m1 and m2 are used for this purpose).
- Check if the count reached (m+n) / 2. If (m+n) is odd return m1, If even return (m1+m2)/2.
// A Simple Merge based O(n) solution to find
// median of two sorted arrays
#include <bits/stdc++.h>
using namespace std;
/* This function returns median of ar1[] and ar2[].
Assumption in this function:
Both ar1[] and ar2[] are sorted arrays */
int getMedian(int ar1[], int ar2[], int n, int m)
{
int i = 0; /* Current index of input array ar1[] */
int j = 0; /* Current index of input array ar2[] */
int count;
int m1 = -1, m2 = -1;
/*loop till (m+n)/2*/
for (count = 0; count <= (m + n)/2; count++)
{
//store (n+m)/2-1 in m2
m2=m1;
if(i != n && j != m)
{
m1 = (ar1[i] > ar2[j]) ? ar2[j++] : ar1[i++];
}
else if(i < n)
{
m1 = ar1[i++];
}
// for case when j<m,
else
{
m1 = ar2[j++];
}
}
// Since there are (n+m) elements,
// There are following two cases
// if n+m is odd then the middle
// index is median i.e. (m+n)/2
// other wise median will be average of elements
// at index ((m+n)/2 - 1) and (m+n)/2
// in the array obtained after merging ar1 and ar2
if((m + n) % 2 == 1){
return m1;
}
else{
return (m1+m2)/2;
}
}
int main()
{
int ar1[] = {900};
int ar2[] = {5,8,10,20};
int n1 = sizeof(ar1)/sizeof(ar1[0]);
int n2 = sizeof(ar2)/sizeof(ar2[0]);
cout << getMedian(ar1, ar2, n1, n2);
}Output:
10
Complexity Analysis: Time Complexity: O(m + n). To merge both the arrays O(m+n) time is needed. Space Complexity: O(1). No extra space is required.
Approach:The idea is simple, calculate the median of both the arrays and discard one half of each array.
Now, there are some basic corner cases. For array size less than or equal to 2
Algorithm :
- Create a recursive function that takes two arrays and the sizes of both the arrays.
- Take care of the base cases for the size of arrays less than 2. (previously discussed in Approach).Note: The first array is always the smaller array.
- Find the middle elements of both the arrays. i.e element at (n – 1)/2 and (m – 1)/2 of first and second array respectively. Compare both the elements.
- If the middle element of the smaller array is less than the middle element of the larger array then the first half of the smaller array is bound to lie strictly in the first half of the merged array. It can also be stated that there is an element in the first half of the larger array and the second half of the smaller array which is the median. So, reduce the search space to the first half of the larger array and the second half of the smaller array.
- Similarly, If the middle element of the smaller array is greater than the middle element of the larger array then reduce the search space to the first half of the smaller array and second half of the larger array.
Implementation:
// A C++ program to find median of two sorted arrays of
// unequal sizes
#include <bits/stdc++.h>
using namespace std;
// A utility function to find median of two integers
float MO2(int a, int b)
{ return ( a + b ) / 2.0; }
// A utility function to find median of three integers
float MO3(int a, int b, int c)
{
return a + b + c - max(a, max(b, c))
- min(a, min(b, c));
}
// A utility function to find a median of four integers
float MO4(int a, int b, int c, int d)
{
int Max = max( a, max( b, max( c, d ) ) );
int Min = min( a, min( b, min( c, d ) ) );
return ( a + b + c + d - Max - Min ) / 2.0;
}
// Utility function to find median of single array
float medianSingle(int arr[], int n)
{
if (n == 0)
return -1;
if (n%2 == 0)
return (double)(arr[n/2] + arr[n/2-1])/2;
return arr[n/2];
}
// This function assumes that N is smaller than or equal to M
// This function returns -1 if both arrays are empty
float findMedianUtil( int A[], int N, int B[], int M )
{
// If smaller array is empty, return median from second array
if (N == 0)
return medianSingle(B, M);
// If the smaller array has only one element
if (N == 1)
{
// Case 1: If the larger array also has one element,
// simply call MO2()
if (M == 1)
return MO2(A[0], B[0]);
// Case 2: If the larger array has odd number of elements,
// then consider the middle 3 elements of larger array and
// the only element of smaller array. Take few examples
// like following
// A = {9}, B[] = {5, 8, 10, 20, 30} and
// A[] = {1}, B[] = {5, 8, 10, 20, 30}
if (M & 1)
return MO2( B[M/2], MO3(A[0], B[M/2 - 1], B[M/2 + 1]) );
// Case 3: If the larger array has even number of element,
// then median will be one of the following 3 elements
// ... The middle two elements of larger array
// ... The only element of smaller array
return MO3( B[M/2], B[M/2 - 1], A[0] );
}
// If the smaller array has two elements
else if (N == 2)
{
// Case 4: If the larger array also has two elements,
// simply call MO4()
if (M == 2)
return MO4(A[0], A[1], B[0], B[1]);
// Case 5: If the larger array has odd number of elements,
// then median will be one of the following 3 elements
// 1. Middle element of larger array
// 2. Max of first element of smaller array and element
// just before the middle in bigger array
// 3. Min of second element of smaller array and element
// just after the middle in bigger array
if (M & 1)
return MO3 ( B[M/2],
max(A[0], B[M/2 - 1]),
min(A[1], B[M/2 + 1])
);
// Case 6: If the larger array has even number of elements,
// then median will be one of the following 4 elements
// 1) & 2) The middle two elements of larger array
// 3) Max of first element of smaller array and element
// just before the first middle element in bigger array
// 4. Min of second element of smaller array and element
// just after the second middle in bigger array
return MO4 ( B[M/2],
B[M/2 - 1],
max( A[0], B[M/2 - 2] ),
min( A[1], B[M/2 + 1] )
);
}
int idxA = ( N - 1 ) / 2;
int idxB = ( M - 1 ) / 2;
/* if A[idxA] <= B[idxB], then median must exist in
A[idxA....] and B[....idxB] */
if (A[idxA] <= B[idxB] )
return findMedianUtil(A + idxA, N/2 + 1, B, M - idxA );
/* if A[idxA] > B[idxB], then median must exist in
A[...idxA] and B[idxB....] */
return findMedianUtil(A, N/2 + 1, B + idxA, M - idxA );
}
// A wrapper function around findMedianUtil(). This function
// makes sure that smaller array is passed as first argument
// to findMedianUtil
float findMedian( int A[], int N, int B[], int M )
{
if (N > M)
return findMedianUtil( B, M, A, N );
return findMedianUtil( A, N, B, M );
}
int main()
{
int A[] = {900};
int B[] = {5, 8, 10, 20};
int N = sizeof(A) / sizeof(A[0]);
int M = sizeof(B) / sizeof(B[0]);
printf("%f", findMedian( A, N, B, M ) );
return 0;
}Output:
10.000000
Complexity Analysis: Time Complexity: O(min(log m, log n)). In each step one half of each array is discarded. So the algorithm takes O(min(log m, log n)) time to reach the median value. Space Complexity: O(1). No extra space is required.
Algorithm:
1. Merge the two given arrays into one array.
2. Then sort the third(merged) array
3. If the length of the third array is even then :
divide the length of array by 2
return arr[value] + arr[value - 1] / 2
4. If the length of the third array is odd then :
divide the length of array by 2
round that value
return the arr[value]
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
int Solution(int arr[], int n)
{
// If length of array is even
if (n % 2 == 0)
{
int z = n / 2;
int e = arr[z];
int q = arr[z - 1];
int ans = (e + q) / 2;
return ans;
}
// If length if array is odd
else
{
int z = round(n / 2);
return arr[z];
}
}
// Driver Code
int main() {
// TODO Auto-generated method stub
int arr1[] = { -5, 3, 6, 12, 15 };
int arr2[] = { -12, -10, -6, -3, 4, 10 };
int i = sizeof(arr1) / sizeof(arr1[0]);
int j = sizeof(arr2) / sizeof(arr2[0]);
int arr3[i+j];
int l = i+j;
// Merge two array into one array
for(int k=0;k<i;k++)
{
arr3[k]=arr1[k];
}
int a=0;
for(int k=i;k<l;k++)
{
arr3[k]=arr2[a++];
}
// Sort the merged array
sort(arr3,arr3+l);
// calling the method
cout<<"Median = " << Solution(arr3, l);
}Output:
Median = 3
Complexity Analysis : Time Complexity: O((n+m) Log (n+m)) Space Complexity: O(n+m). Since we are creating a new array of size n+m.
Algorithm:
1. Lets assume that there are two arrays A and B with array A having the minimum number of elements.
If this is not the case then swap A and B to make A having small size.
2. The edge cases like one array is empty or both are empty will be handled.
3. let n be the size of A and m be the size of B.
Now think of an idea that if we have to find the median than we have to divide the whole merged array into two parts
namely left and right parts.
Now since we are given the size of left part (i.e (n+m+1)/2), Now look at below given example.
A-> 1,2,3,4,5 n = 5
B-> 1,2,3,4,5,6 m = 6
Here merged array will look like :- 1,1,2,2,3,3,4,4,5,5,6 and median then is 3
Now we can see our left part which is underlined. We divide A and B into two parts such that the
sum of left part of both A and B will result in left part of merged array.
A-> 1,2,3,4,5 // pointers l =0 and r = n-1 hence mid = (l+r)/2;
B -> 1,2,3,4,5,6
we can see that left part of A is given as n/2 and since total length of left part in merged array
is (m+n+1)/2, so left part of B = (m+n+1)/2-n/2;
Now we just have to confirm if our left and right partitions in A and B are correct or not.
4. Now we have 4 variables indicating four values two from array A and two from array B.
leftA -> Rightmost element in left part of A = 2
leftb -> Rightmost element in left part of B = 4
rightA -> Leftmost element in right part of A = 3
rightB -> Leftmost element in right part of B = 5
Hence to confirm that partition is correct we have to check the following conditions.
leftA<=rightB and leftB<=rightA // This is the case when the sum of two parts of A and B results in left part of merged array
if our partition not works that means we have to find other mid point in A and then left part in B
This is seen when
leftA > rightB //means we have to dec size of A's partition
so do r = mid-1;
else
do l =mid+1;
Hence repeat the above steps with new partitions till we get the answers.
5. If leftA<=rightB and leftB<=rightA
then we get correct partition and our answer depends on the total size of merged array (i.e. m+n)
If (m+n)%2==0
ans is max(leftA,leftB)+min(rightA,rightB)/2; // max of left part is nearest to median and min of right part is nearest to medain
else
ans is max(leftA,leftB);
Hence the above algorithm can be coded as
#include <bits/stdc++.h>
using namespace std;
// Method to find median
double Median(vector<int>& A, vector<int>& B)
{
int n = A.size();
int m = B.size();
if (n > m)
return Median(B, A); // Swapping to make A smaller
int start = 0;
int end = n;
int realmidinmergedarray = (n + m + 1) / 2;
while (start <= end) {
int mid = (start + end) / 2;
int leftAsize = mid;
int leftBsize = realmidinmergedarray - mid;
int leftA
= (leftAsize > 0)
? A[leftAsize - 1]
: INT_MIN; // checking overflow of indices
int leftB
= (leftBsize > 0) ? B[leftBsize - 1] : INT_MIN;
int rightA
= (leftAsize < n) ? A[leftAsize] : INT_MAX;
int rightB
= (leftBsize < m) ? B[leftBsize] : INT_MAX;
// if correct partition is done
if (leftA <= rightB and leftB <= rightA) {
if ((m + n) % 2 == 0)
return (max(leftA, leftB)
+ min(rightA, rightB))
/ 2.0;
return max(leftA, leftB);
}
else if (leftA > rightB) {
end = mid - 1;
}
else
start = mid + 1;
}
return 0.0;
}
// Driver code
int main()
{
vector<int> arr1 = { -5, 3, 6, 12, 15 };
vector<int> arr2 = { -12, -10, -6, -3, 4, 10 };
cout << "Median of the two arrays are" << endl;
cout << Median(arr1, arr2);
return 0;
}Output:
Median of the two arrays are 3
Time Complexity: O(min(log m, log n)) : Since binary search is being applied on the smaller of the 2 arrays Auxiliary Space: O(1)