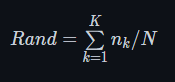Skip to content

Latest commit

 

History

History
67 lines (43 loc) · 2.8 KB

README.md

File metadata and controls

67 lines (43 loc) · 2.8 KB

K-means

k means算法及其优化方式

k-means算法本身不难,很比较好理解,整体的思路为:

  1. 随机选择聚类中心
  2. 将所有点与聚类中心计算距离,找到最小的距离的聚类中心,聚簇
  3. 重新计算每个簇的平均点的位置,更新为该簇的聚类中心
  4. 如果聚类中心不变,则认为聚类成功,结束. 否则回到步骤2

由于本身算法较为简单直接,不再赘述. 但是纯 k-means 存在很多局限性,比如初始点的选择? 计算时间复杂度? 聚类效果? 本身由于其算法局限性我们也要考虑很多问题

  1. 聚类点的簇内无点? -> 重新随机选择聚类中心(k-means.py)
  2. 维度过高计算量太大? -> PCA降维
  3. 如果聚类数量 K 不作为先验知识, 如果这种无监督的聚类方法能否自己找到合适的聚类数量? -> 强化学习?
  4. 聚类效果如何评价? -> kappa

由此衍生出了一些改进的 K-means 算法,比如 rough k-means,带权 k-means, 与蚁群算法结合等等

Use

cd homework-2/k-means
python main.py -r

arguments:

  • -r(optional): 随机生成数据,由于参数众多没有使用命令行传参,相关配置信息在config.yaml

    不选择此项时采用默认标准 k-means 数据集 UCI Balance-scale和Iris,由于数据维度较高没有使用可视化

    选择此项时使用生成的数据集,相关参数为,可根据需要自行调整:

    • NAME: "example" 数据保存位置
    • K: 5 : 分类数量
    • SIZE: 100 每组数量
    • RANGE: 数据范围
      • min: 0
      • max: 200
    • RADIUS: 50 数据分布距离中心点范围

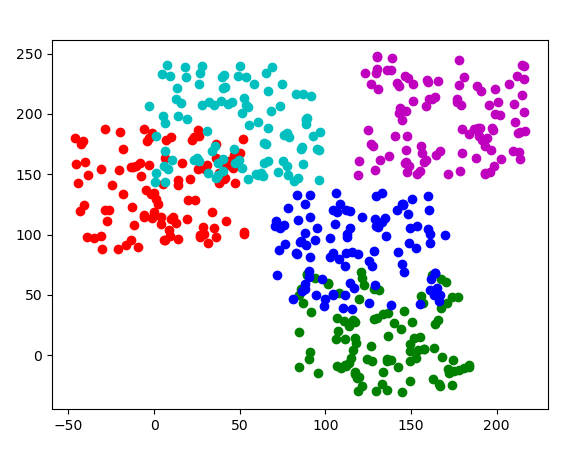
这是一次随机生成的数据

20220410173633

之后下方会出现提示,如果认为该数据生成的不够理想选择 y 重新生成, 如果满意的话输入 n 开始聚类

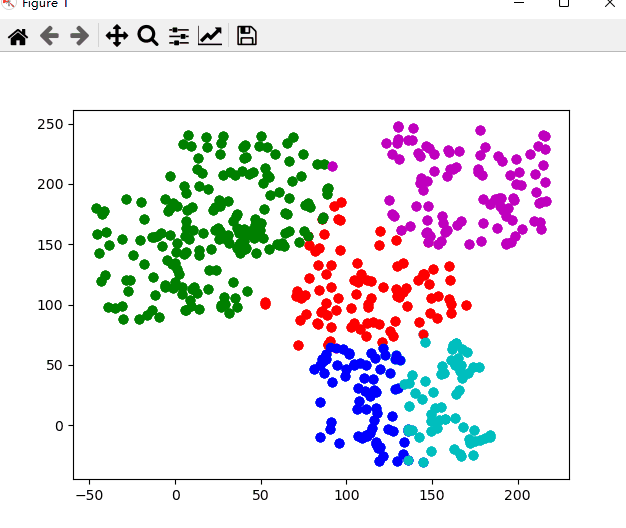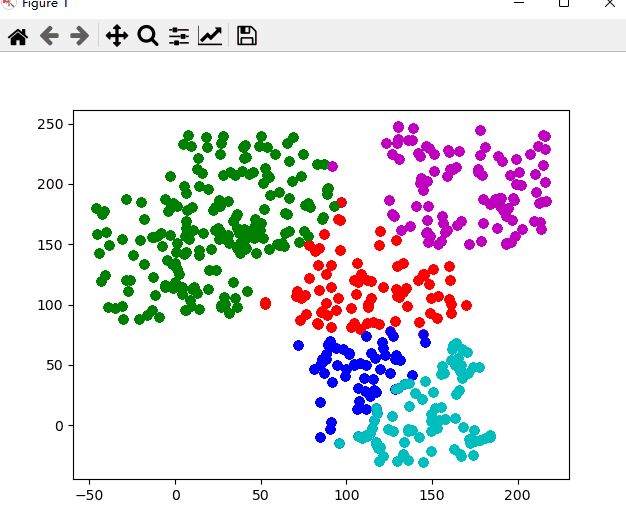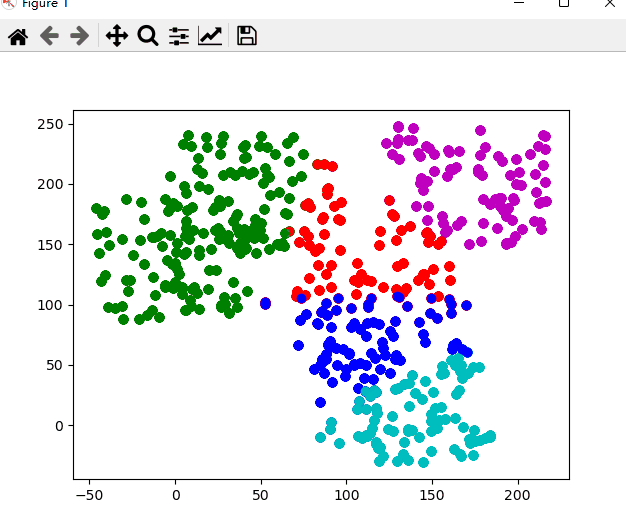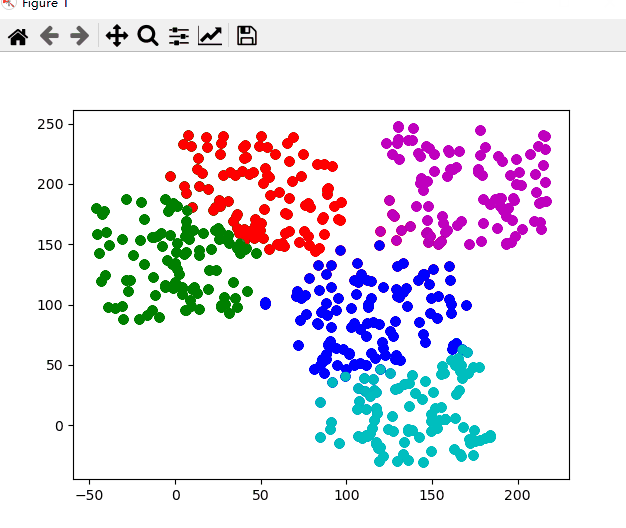
Does the data satisfy? Do you want to restart?(y/n)

以下是该次聚类的动态图,聚类的过程也就是 k-means 算法的过程

kmeans

Evaluation

limits_{k=1}^Kn_kN

nk表示正确划入第 k 簇中样本的个数,聚类结果中任意一个簇的下近似中,若其中含有k类别的样本数目最多,则认为该集合为第K类数据的分布.

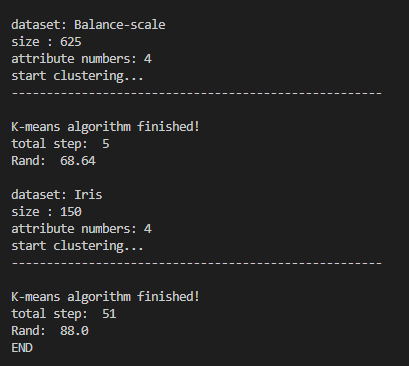
对于两个标准数据集,由于初始点的选择不同有可能有不同的 Rand 值,以下是我在两个数据集中计算得到的 Rand 值

20220410193742