Hidden Markov Model
from [1]():
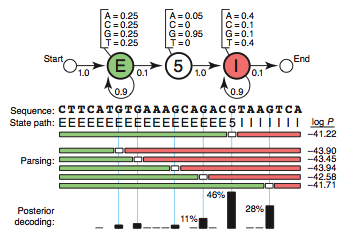
Each state has its own emission probabilities, which, for example, models the base composition of exons, introns and the consensus G at the 5′SS.
Each state also has transition probabilities, the probabilities of moving from this state to a new state.
The Baum–Welch algorithm is used to find the unknown parameters of a hidden Markov model (HMM). [2] I.e. given a sequence of observations, generate a transition and emission matrix that may have generated the observations. [4]
The BWA makes use of the forward-backward algorithm. [2]
There are potentially many state paths that could generate the same sequence. We want to find the one with the highest probability. (...) The efficient Viterbi algorithm is guaranteed to find the most probable state path given a sequence and an HMM. [1] The Baum–Welch algorithm uses the well known EM algorithm to find the maximum likelihood estimate of the parameters of a hidden Markov model given a set of observed feature vectors. [3]
HMMs don’t deal well with correlations between residues, because they assume that each residue depends only on one underlying state. [1]
interactive spreasheet for teaching forward-backward algorithm