| layout | mathjax | permalink |
|---|---|---|
page |
true |
classificacaoLinear/ |
Tabela de Conteúdos:
- O que faremos em seguida
- Definindo uma função de resultados
- Interpretando um classificador linear
- Definindo uma função de perdas
- Perdas de máquinas de vetores suporte para várias classes
- Hora de estudar código Java e testar
Dica: Após visitar um link da tabela de conteúdos, utilize a tecla de retorno do seu navegador para voltar para a tabela.
Na aula anterior foi introduzido o problema de classificar images. Estudamos também dois algorítimos, o vizinho mais próximo e o k-vizinho mais próximo, capazes de lidar com a tarefa. Estes algorítimos, porém, apresentam uma série de desvantagens, além do fraco desempenho. Para cada classificação (uma imagem de teste), precisam comparar a imagem com todas as imagens do treino. Podemos dizer que não existe ganho de generalização em cada treino que eles fazem.
Vamos em seguida desenvolver uma abordagem mais poderosa, e que eventual e naturalmente poderá ser estendida para algorítimos que utilizam redes neurais e redes convolucionais. A base desta nova abordagem vão ser duas funções. A primeira, uma função de resultados, parametrizada, encarregada de mapear uma imagem para o rótulo que a classifica. A segunda, uma função de perdas, também chamada função de custo, que verifica as predições de resultados contra os resultados reais de cada imagem. Podemos considerar portanto que usamos a função de perda para medir a eficiência dos pesos (parâmetros) utilizados pela função de resultados em sua tarefa. Passaremos então a tratar estes valores obtidos como um problema de minimação, ou seja, vamos tentar minimizar a função de perdas com relação aos parâmetros da função de resultados.
Devemos começar esta abordagem definindo a função de resultados, que mapeia os valores dos pixeis de uma imagem para percentuais de confiança
de resultados de classificação possíveis de cada classe. Vamos desenvolver a abordagem com um exemplo concreto. Vamos considerar um conjunto de
imagens de treino
Isto significa que temos n exemplos (cada um com dimensionalidade d) e k categorias distintas. No caso do CIFAR-10,
por exemplo, temos um conjunto de treinamento com n = 50000 imagens, cada uma com d = 32X32X3 = 3072 pixeis, e k = 10,
já que existem 10 classes distintas (cachorro, gato, carro, etc).Vamos definir em seguida a função de resultados,
Nesta lição vamos começar com o que pode ser considerada a função mais simples, um classificador linear:
Na equação acima, estamos assumindo que a imagem
Observações importantes:
- Note que a multiplicação de matriz única
$$Wx_i$$ está efetivamente calculando 10 classificadores distintos em paralelo, (um para cada classe), onde cada classificador é uma linha de W. - Note também que consideramos os dados de entrada
$$(x_i, y_i)$$ como dados e fixo, porém, temos controle sobre a atribuição dos valores dos parâmetros W,b. Nosso objetivo é atribuir estes valores de tal forma que os resultados da função coincidam com os valores reais da classificação das imagens em todo o conjunto de entrada. Teremos que aprofundar bastante aqui, mas podemos inicialmente construir a ideia de que desejamos que a classe correta tenha maior valor nos resultados do que as demais classes (as erradas). - Uma vantagem desta abordagem é que os dados de treinamento são utilizados para aprender os parâmetros W,b, mas, uma vez que a aprendizagem estiver completa, podemos descartar os dados de treino e guardar apenas os parâmetros.Uma imagem de teste pode apenas ser inserida na função e sua classificação baseada nos resultados obtidos.
- Por último, observemos que para classificar uma imagem de teste basta uma multiplicação e adição de matriz, o que é significativamente mais rápido do que comparar cada pixel da imagem com cada pixel de todas as imagens do conjunto de treino.
Um classificador linear calcula o resultado de uma classe através de uma soma, na qual se coloca pesos, dos valores dos pixeis de uma imagem ao longo de cada um dos seus três canais de cores. Dependendo dos valores que atribuímos a estes pesos, a função tem a capacidade de concordar ou discordar (dependendo do sinal do peso) de certas cores em determinadas posições da imagem. Por exemplo, podemos imaginar que um navio tende a ter quantidades de azul em ambos os lados de sua imagem, correspondentes a água. Portanto, um classificador de navio deve ter mais pesos positivos no canal azul nas posições ao laterais (presença de azul aumenta o resultado navio), e menos pesos negativos nos canais vermelho e verde nas mesmas posições (presença de verde e vermelho diminuem o resultado navio).
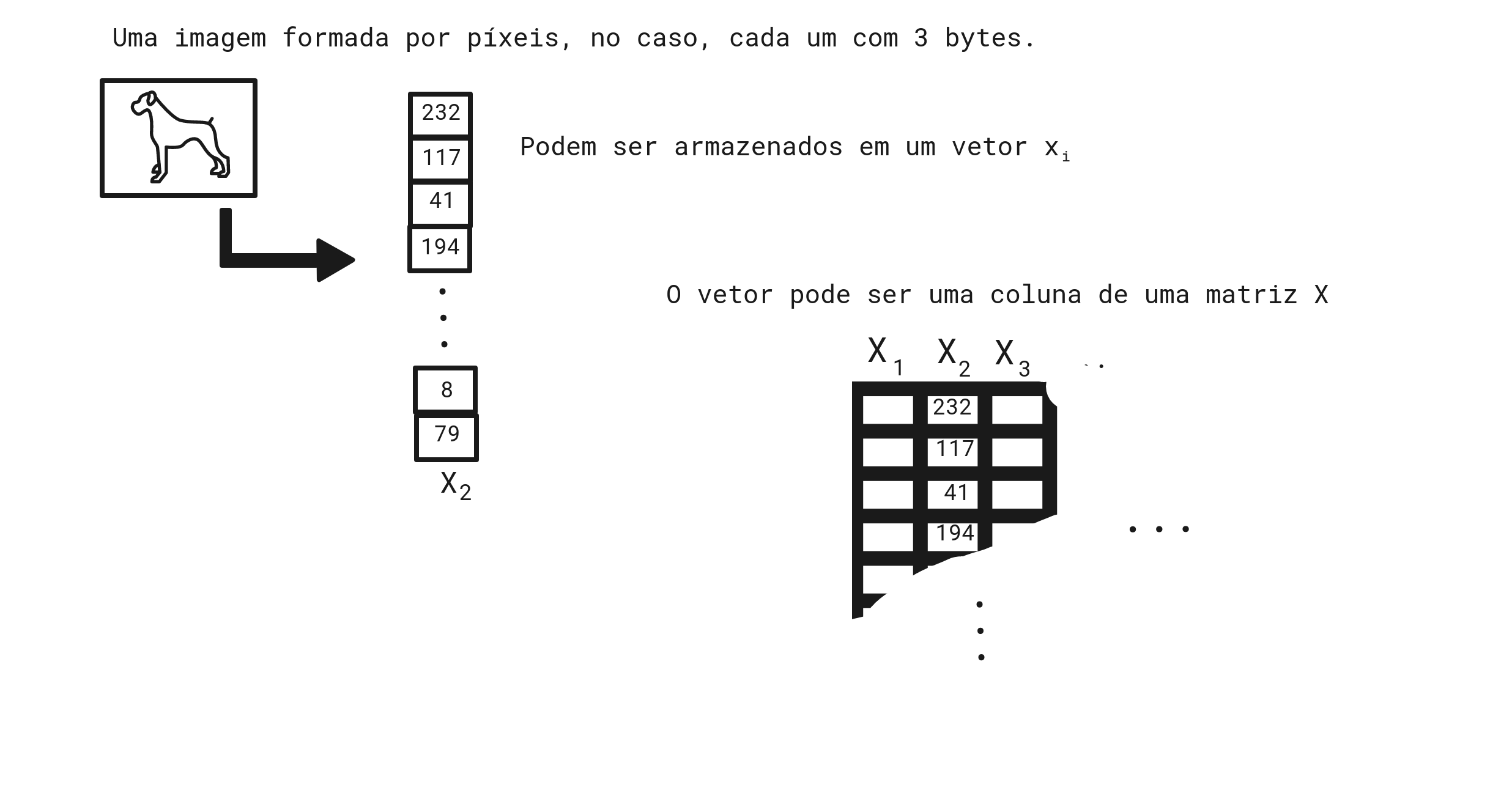
No caso do CIFAR-10, armazenamos 50000 imagens de treino, cada uma com 3072 bytes, em uma matriz X de dimensões [50000 x 3072]. Armazenamos os pesos em uma matriz W, com dimensões [10 x 3072]. Finalmente, armazenamos o bias em um vetor b de dimensão [10 x 1].
A operação de classificação que desejamos executar consistem em multiplicar W por X e somar b.
Como vimos anteriormente, armazenamos em W 10 linhas de pesos, cada linha com 3072 colunas, ou seja, uma coluna
para cada byte da imagem, uma linha para cada classe existente. Os valores dos pesos em W serão gradualmente
ajustados para que, gradativamente os pesos de uma linha fiquem adequados para classificar corretamente determinado
tipo de imagem.
Podemos executar a operação
Como mencionamos acima, podemos realizar a operação de três formas:
- A primeira consiste em utilizar duas repetições aninhadas, uma para linhas e outra para colunas, e fazer a multiplicação elemento por elemento.
- A segunda consiste em utilizar uma repetição para visitar cada linha de X, atribuindo cada linha a um
vetor
$$X_i$$ , e calculando o produto$$WX_i$$ que será um vetor de resultados. - Por último, com o máximo de paralelismo, O truque do bias simplifica nossa operação para
$$WX^T$$ . Observe que$$X^T$$ é a matriz X transposta, ou seja, com linhas e colunas invertidas, para que a regra de produto de matrizes seja satisfeita. Em seguida, transpomos o produto obtido para avaliar a matriz Resultados de forma conveniente. As duas últimas formas são mais vantajosas se forem utilizadas APIs de operações com matrizes que ofereçam otimização real para as operações. Mesmo quando isto não ocorre em nossos exemplos, o foco é aprender como a operação otimizada funciona, para poder futuramente obter vantagem de bibliotecas especializadas com otimizações.
Nos exemplos que mencionamos até agora temos utilizado o valor original dos bytes dos pixeis das imagens, que varia na faixa [0...255]. Uma prática comum porém é normalizar os valores dos atributos (cada pixel pode ser considerado um atributo). Uma prática importante é centralizar os dados, subtraindo a média dos atributos de cada atributo. No caso de imagens resultará em dados aproximadamente na faixa [-127...127]. É comum também escalar os atributos para a faixa [-1...1]. Centralizar os atributos em 0 é bastante importante para o método do gradiente descendente que veremos mais adiante.
Na seção anterior definimos uma função que mapeia pixeis de imagens para resultados de classes, parametrizada por um conjunto de pesos W. Vimos também que apesar de não termos controle sobre os pixeis (que são fixos, característicos de cada imagem), temos controle sobre os pesos W, que desejamos ir ajustando para que nossas predições coincidam com os resultados das classes a que cada imagem pertence.
Podemos imaginar aqui que, como os valores iniciais dos pesos são atribuídos de forma aleatória, não devem inicialmente funcionar de forma muito boa. Podemos esperar que, ao classificar uma imagem de um cachorro, esta obtenha uma pontuação baixa no classificador de cachorro, e pontuações altas nos classificadores de caminhão e carro. Ora, assim nossos classificadores estariam achando que o cachorro é um caminhão ou um carro.
Nós vamos medir o grau de erro de classificações como esta utilizando uma função de perdas (também chamada de função de custos ou objetivo). Intuitivamente, a perda deve aumentar quanto mais errada for a classificação, e deve ser pequena para classificações melhores. Esta graduação traduz o fato de que é menos errado confundir um cachorro com um gato do que confundir um sapo com um navio.
Dentre as várias formas de calcular perdas, abordaremos inicialmente a perda de máquinas de vetores suporte. O cálculo
busca fazer com que a classe correta de uma classificação pontue melhor que uma classe errada por no mínimo uma
determinada margem de valor
Visite a área de código do projeto, estude a classe LinearPrediction.java.
Observe que existem três métodos para calcular a perda:
public double lossFunctionUnvectorized(RealMatrix X, RealVector Y, RealMatrix W);
public double lossFunctionSemivectorized(RealMatrix X, RealVector Y, RealMatrix W);
public double lossFunctionFullvectorized(RealMatrix X, RealVector Y, RealMatrix W)
Cada um deles implementa uma das formas de operação mencionadas acima, ou seja, a versão não vetorizada executa duas repetições aninhadas para visitar cad elemento das matrizes, a versão semivetorizada utiliza uma repetição para extrair um vetor de cada linha da matriz X (cada vetor portanto possui os bytes de uma imagem), e a versão plenamente vetorizada realiza a operação linear através de um único produto de matrizes.