DAY10P1.md

Rotting Oranges

---

• Question:

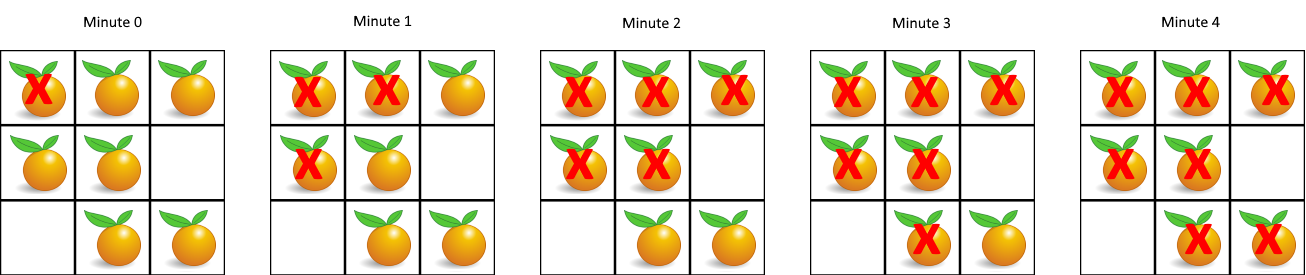
You are given an m x n grid where each cell can have one of three values:

• 0 representing an empty cell,
• 1 representing a fresh orange, or
• 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

---

• Example:

Input: grid = [[2,1,1],[1,1,0],[0,1,1]]

Output: 4

---

• Solution:

Code :

class Solution {
    public int orangesRotting(int[][] grid) {
        if(grid == null || grid.length == 0) return 0;
        int rows = grid.length;
        int cols = grid[0].length;
        Queue<int[]> queue = new LinkedList<>();
        int count_fresh = 0;
        //Put the position of all rotten oranges in queue
        //count the number of fresh oranges
        for(int i = 0 ; i < rows ; i++) {
            for(int j = 0 ; j < cols ; j++) {
                if(grid[i][j] == 2) {
                    queue.offer(new int[]{i , j});
                }
                else if(grid[i][j] == 1) {
                    count_fresh++;
                }
            }
        }
        //if count of fresh oranges is zero --> return 0 
        if(count_fresh == 0) return 0;
        int count = 0;
        int[][] dirs = {{1,0},{-1,0},{0,1},{0,-1}};
        //bfs starting from initially rotten oranges
        while(!queue.isEmpty()) {
            ++count;
            int size = queue.size();
            for(int i = 0 ; i < size ; i++) {
                int[] point = queue.poll();
                for(int dir[] : dirs) {
                    int x = point[0] + dir[0];
                    int y = point[1] + dir[1];
                    //if x or y is out of bound
                    //or the orange at (x , y) is already rotten
                    //or the cell at (x , y) is empty
                        //we do nothing
                    if(x < 0 || y < 0 || x >= rows || y >= cols || grid[x][y] == 0 || grid[x][y] == 2) continue;
                    //mark the orange at (x , y) as rotten
                    grid[x][y] = 2;
                    //put the new rotten orange at (x , y) in queue
                    queue.offer(new int[]{x , y});
                    //decrease the count of fresh oranges by 1
                    count_fresh--;
                }
            }
        }
        return count_fresh == 0 ? count-1 : -1;
    }
}