https://leetcode-cn.com/problems/max-chunks-to-make-sorted-ii/
这个问题和“最多能完成排序的块”相似,但给定数组中的元素可以重复,输入数组最大长度为2000,其中的元素最大为10**8。
arr是一个可能包含重复元素的整数数组,我们将这个数组分割成几个“块”,并将这些块分别进行排序。之后再连接起来,使得连接的结果和按升序排序后的原数组相同。
我们最多能将数组分成多少块?
示例 1:
输入: arr = [5,4,3,2,1]
输出: 1
解释:
将数组分成2块或者更多块,都无法得到所需的结果。
例如,分成 [5, 4], [3, 2, 1] 的结果是 [4, 5, 1, 2, 3],这不是有序的数组。
示例 2:
输入: arr = [2,1,3,4,4]
输出: 4
解释:
我们可以把它分成两块,例如 [2, 1], [3, 4, 4]。
然而,分成 [2, 1], [3], [4], [4] 可以得到最多的块数。
注意:
arr的长度在[1, 2000]之间。
arr[i]的大小在[0, 10**8]之间。
- 栈
- 队列
这里可以使用类似计数排序的技巧来完成。以题目给的 [2,1,3,4,4] 来说:
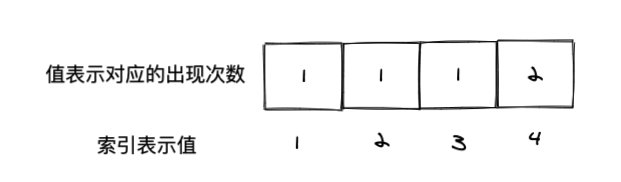
可以先计数,比如用一个数组来计数,其中数组的索引表示值,数组的值表示其对应的出现次数。比如上面,除了 4 出现了两次,其他均出现一次,因此 count 就是 [0,1,1,1,2]。
其中 counts[4] 就是 2,表示的就是 4 这个值出现了两次。
实际上 count 最开始的 0 是没有必要的,不过这样方便理解罢了。
如果我们使用数组来计数,那么空间复杂度就是
计数完毕之后, 我们要做的是比较当前的 arr 和最终的 arr(已经有序的 arr) 的计数数组的关系即可。
这里有一个关键点: 如果两个数组的计数信息是一致的,那么两个数组排序后的结果也是一致的。 如果你理解计数排序,应该明白我的意思。不明白也没有关系, 我稍微解释一下你就懂了。
如果我把一个数组打乱,然后排序,得到的数组一定是确定的,即不管你怎么打乱排好序都是一个确定的有序序列。这个论点的正确性是毋庸置疑的。而实际上,一个数组无论怎么打乱,其计数结果也是确定的,这也是毋庸置疑的。反之,如果是两个排序后不同的数组,打乱排序后的结果一定是不同的,计数也是同理。
因此我们的算法有了:
- 先排序 arr,不妨记排序后的 arr 为 sorted_arr
- 从左到右遍历 arr,比如遍历到了索引为 i 的元素,其中 0 <= i < len(arr)
- 如果 arr[:i+1] 的计数信息和 sorted_arr[:i+1] 的计数信息一致,那么说明可以贪心地切分,否则一定不可以分割。
arr[:i+1] 指的是 arr 的切片,从索引 0 到 索引 i 的一个切片。
- 计数
- 语言支持:Python
Python Code:
class Solution(object):
def maxChunksToSorted(self, arr):
count_a = collections.defaultdict(int)
count_b = collections.defaultdict(int)
ans = 0
for a, b in zip(arr, sorted(arr)):
count_a[a] += 1
count_b[b] += 1
if count_a == count_b: ans += 1
return ans复杂度分析
- 时间复杂度:内部 count_a 和 count_b 的比较时间复杂度也是
$O(N)$ ,因此总的时间复杂度为$O(N^2)$ ,其中 N 为数组长度。 - 空间复杂度:使用了两个 counter,其大小都是 N,因此空间复杂度为
$O(N)$ ,其中 N 为数组长度。
实际上,我们不需要两个 counter ,而是使用一个 counter 来记录 arr 和 sorted_arr 的 diff 即可。但是这也仅仅是空间上的一个常数优化而已。
我们还可以在时间上进一步优化, 去除内部 count_a 和 count_b 的比较,这样算法的瓶颈就是排序了。而去除的关键点就是我们上面提到的记录 diff,具体参考下方代码。
- 计数
- count 的边界条件
- 语言支持:Python
Python Code:
class Solution(object):
class Solution(object):
def maxChunksToSorted(self, arr):
count = collections.defaultdict(int)
non_zero_cnt = 0
ans = 0
for a, b in zip(arr, sorted(arr)):
if count[a] == -1: non_zero_cnt -= 1
if count[a] == 0: non_zero_cnt += 1
count[a] += 1
if count[b] == 1: non_zero_cnt -= 1
if count[b] == 0: non_zero_cnt += 1
count[b] -= 1
if non_zero_cnt == 0: ans += 1
return ans复杂度分析
- 时间复杂度:瓶颈在于排序,因此时间复杂度为
$O(NlogN)$ ,其中 N 为数组长度。 - 空间复杂度:使用了一个 counter,其大小是 N,因此空间复杂度为
$O(N)$ ,其中 N 为数组长度。
通过题目给的三个例子,应该可以发现一些端倪。
- 如果 arr 是非递减的,那么答案为 1。
- 如果 arr 是非递增的,那么答案是 arr 的长度。
并且由于只有分的块内部可以排序,块与块之间的相对位置是不能变的。因此直观上我们的核心其实找到从左到右开始不减少(增加或者不变)的地方并分块。
比如对于 [5,4,3,2,1] 来说:
- 5 的下一个是 4,比 5 小,因此如果分块,那么永远不能变成[1,2,3,4,5]。
- 同理,4 的下一个是 3,比 4 小,因此如果分块,那么永远不能变成[1,2,3,4,5]。
- 。。。
最后就是不能只能是整体是一个大块,我们返回 1 即可。
我们继续分析一个稍微复杂一点的,即题目给的 [2,1,3,4,4]。
- 2 的下一个是 1,比 2 小,不能分块。
- 1 的下一个是 3,比 1 大,可以分块。
- 3 的下一个是 4,比 3 大,可以分块。
- 4 的下一个是 4,一样大,可以分块。
因此答案就是 4,分别是:
- [2,1]
- [3]
- [3]
- [4]
然而上面的算法步骤是不正确的,原因在于只考虑局部,没有考虑整体,比如 [4,2,2,1,1] 这样的测试用例,实际上只应该返回 1,原因是后面碰得到了 1,使得前面不应该分块。
因为把数组分成数个块,分别排序每个块后,组合所有的块就跟整个数组排序的结果一样,这就意味着后面块中的最小值一定大于前面块的最大值,这样才能保证分块有。因此直观上,我们又会觉得是不是”只要后面有较小值,那么前面大于它的都应该在一个块里面“,实际上的确如此。
有没有注意到我们一直在找下一个比当前小的元素?这就是一个信号,使用单调递增栈即可以空间换时间的方式解决。对单调栈不熟悉的小伙伴可以看下我的单调栈专题
不过这还不够,我们要把思路逆转!
这是《逆转裁判》 中经典的台词, 主角在深处绝境的时候,会突然冒出这句话,从而逆转思维,寻求突破口。
这里的话,我们将思路逆转,不是分割区块,而是融合区块。
比如 [2,1,3,4,4],遍历到 1 的时候会发现 1 比 2 小,因此 2, 1 需要在一块,我们可以将 2 和 1 融合,并重新压回栈。那么融合成 1 还是 2 呢?答案是 2,因为 2 是瓶颈,这提示我们可以用一个递增栈来完成。
为什么 2 是瓶颈?因此我们需要确保当前值一定比前面所有的值的最大值还要大。因此只需要保留最大值就好了,最大值就是瓶颈。而 1 和 2 的最大值是 2,因此 2 就是瓶颈。
因此本质上栈存储的每一个元素就代表一个块,而栈里面的每一个元素的值就是块的最大值。
以 [2,1,3,4,4] 来说, stack 的变化过程大概是:
- [2]
- 1 被融合了,保持 [2] 不变
- [2,3]
- [2,3,4]
- [2,3,4,4]
简单来说,就是将一个减序列压缩合并成最该序列的最大的值。 因此最终返回 stack 的长度就可以了。
具体算法参考代码区,注释很详细。
- 语言支持:Python,CPP,Java,JS, Go, PHP
Python Code:
class Solution:
def maxChunksToSorted(self, A: [int]) -> int:
stack = []
for a in A:
# 遇到一个比栈顶小的元素,而前面的块不应该有比 a 小的
# 而栈中每一个元素都是一个块,并且栈的存的是块的最大值,因此栈中比 a 小的值都需要 pop 出来
if stack and stack[-1] > a:
# 我们需要将融合后的区块的最大值重新放回栈
# 而 stack 是递增的,因此 stack[-1] 是最大的
cur = stack[-1]
# 维持栈的单调递增
while stack and stack[-1] > a: stack.pop()
stack.append(cur)
else:
stack.append(a)
# 栈存的是块信息,因此栈的大小就是块的数量
return len(stack)
CPP Code:
class Solution {
public:
int maxChunksToSorted(vector<int>& arr) {
stack<int> stack;
for(int i =0;i<arr.size();i++){
// 遇到一个比栈顶小的元素,而前面的块不应该有比 a 小的
// 而栈中每一个元素都是一个块,并且栈的存的是块的最大值,因此栈中比 a 小的值都需要 pop 出来
if(!stack.empty()&&stack.top()>arr[i]){
// 我们需要将融合后的区块的最大值重新放回栈
// 而 stack 是递增的,因此 stack[-1] 是最大的
int cur = stack.top();
// 维持栈的单调递增
while(!stack.empty()&&stack.top()>arr[i]){
sstackta.pop();
}
stack.push(cur);
}else{
stack.push(arr[i]);
}
}
// 栈存的是块信息,因此栈的大小就是块的数量
return stack.size();
}
};JAVA Code:
class Solution {
public int maxChunksToSorted(int[] arr) {
LinkedList<Integer> stack = new LinkedList<Integer>();
for (int num : arr) {
// 遇到一个比栈顶小的元素,而前面的块不应该有比 a 小的
// 而栈中每一个元素都是一个块,并且栈的存的是块的最大值,因此栈中比 a 小的值都需要 pop 出来
if (!stack.isEmpty() && num < stack.getLast()) {
// 我们需要将融合后的区块的最大值重新放回栈
// 而 stack 是递增的,因此 stack[-1] 是最大的
int cur = stack.removeLast();
// 维持栈的单调递增
while (!stack.isEmpty() && num < stack.getLast()) {
stack.removeLast();
}
stack.addLast(cur);
} else {
stack.addLast(num);
}
}
// 栈存的是块信息,因此栈的大小就是块的数量
return stack.size();
}
}JS Code:
var maxChunksToSorted = function (arr) {
const stack = [];
for (let i = 0; i < arr.length; i++) {
a = arr[i];
if (stack.length > 0 && stack[stack.length - 1] > a) {
const cur = stack[stack.length - 1];
while (stack && stack[stack.length - 1] > a) stack.pop();
stack.push(cur);
} else {
stack.push(a);
}
}
return stack.length;
};Go Code:
func maxChunksToSorted(arr []int) int {
var stack []int // 单调递增栈, stack[-1] 栈顶
for _, a := range arr {
// 遇到一个比栈顶小的元素,而前面的块不应该有比 a 小的
// 而栈中每一个元素都是一个块,并且栈的存的是块的最大值,因此栈中比 a 小的值都需要 pop 出来
if len(stack) > 0 && stack[len(stack)-1] > a {
// 我们需要将融合后的区块的最大值重新放回栈
// 而 stack 是递增的,因此 stack[-1] 是最大的
cur := stack[len(stack)-1]
// 维持栈的单调递增
for len(stack) > 0 && stack[len(stack)-1] > a {
stack = stack[:len(stack)-1] // pop
}
stack = append(stack, cur) // push
} else {
stack = append(stack, a) // push
}
}
// 栈存的是块信息,因此栈的大小就是块的数量
return len(stack)
}PHP Code:
class Solution
{
/**
* @param Integer[] $arr
* @return Integer
*/
function maxChunksToSorted($arr)
{
$stack = []; // 单调递增栈, stack[-1] 栈顶
foreach ($arr as $a) {
// 遇到一个比栈顶小的元素,而前面的块不应该有比 a 小的
// 而栈中每一个元素都是一个块,并且栈的存的是块的最大值,因此栈中比 a 小的值都需要 pop 出来
if ($stack && $stack[count($stack) - 1] > $a) {
$cur = $stack[count($stack) - 1];
// 维持栈的单调递增
while ($stack && $stack[count($stack) - 1] > $a) array_pop($stack);
array_push($stack, $cur);
} else array_push($stack, $a);
}
// 栈存的是块信息,因此栈的大小就是块的数量
return count($stack);
}
}复杂度分析
- 时间复杂度:$O(N)$,其中 N 为数组长度。
- 空间复杂度:$O(N)$,其中 N 为数组长度。
实际上本题的单调栈思路和 【力扣加加】从排序到线性扫描(57. 插入区间) 以及 394. 字符串解码 都有部分相似,大家可以结合起来理解。
融合与【力扣加加】从排序到线性扫描(57. 插入区间) 相似, 重新压栈和 394. 字符串解码 相似。
大家对此有何看法,欢迎给我留言,我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库:https://github.com/azl397985856/leetcode 。 目前已经 37K star 啦。
大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。